Как посчитать процент от суммы

Способ третий: считаем на калькуляторе

Если сомневаетесь в своих математических способностях, то воспользуйтесь калькулятором. С его помощью считается быстрее и точнее, особенно если речь идёт о больших суммах. Проще работать с калькулятором, у которого есть кнопка со знаком процент %. Сумму умножаем на количество процентов и нажимаем кнопку %. На экране высветится необходимый ответ.

Например, вы хотите посчитать, каким будет ваше пособие по уходу за ребёнком до 1,5 лет. Оно составляет 40% от среднего заработка за два последних закрытых календарных года. Допустим, средняя зарплата получилась 30 000 рублей. На калькуляторе 30 000 умножаем на 40 и нажимаем кнопку %. Клавишу = трогать не нужно. На экране высветится ответ 12 000. Это и будет величина пособия.

Как видите, всё очень просто. Тем более, что приложение «Калькулятор» сейчас есть в каждом сотовом телефоне. Если специальной кнопки % у аппарата нет, то воспользуйтесь одним из двух описанных выше способов. А умножение и деление произведите на калькуляторе, что облегчит и ускорит ваши вычисления.

Не забудьте: для облегчения подсчётов есть онлайн-калькуляторы. Действуют они так же, как и обычные, но всегда под рукой, когда вы работаете на компьютере.

Делим на 100

Если разделить число на сто, вы получите числовой эквивалент равный 1%. Чтобы дальше найти процент от суммы, умножьте на 1%, а чтобы перевести число в проценты, разделите на 1%.

Например, вы хотите купить чай по акции. Его обычная цена 150 рублей, а сейчас на него действует скидка 7%. Однако, у вас также есть карта данного магазина, и по ней чай будет стоить 132 рубля. Какой из вариантов выгоднее?

Переведите 7% в рубли. Для этого разделите сначала 150 на 100. Получается, 1% равен 1,5 рубля. Теперь умножаем 1,5 на 7, выходит 10,5 рублей. Вычитаем из полной стоимости чая полученную скидку в рублях. Выходит, что цена чая со скидкой – 139,5 рубля. Значит, выгоднее купить товар по карте.

Другой пример. Вы зашли на сайт и видите, что вещь, которая вам давно приглянулась стоит 2000 вместо 3000. Посчитаем, сколько составила скидка. Итак, делим 3000 на 100 и получаем 30. Это 1% старой цены. Теперь новую цену, то есть 2000 делим 1%. 2000/30 = 66,6666%

100 – 66,6666 = 33,3333% — размер скидки, которую предоставил магазин.

Как просчитать процент на калькуляторе

Можно рассчитать процент и онлайн. Это простой и удобный способ. При этом нужно зайти в интернет и найти калькулятор.

Затем в поля нужно ввести запрашиваемые данные и получить результат. При этом можно узнать, как % от общего числа, так и сколько процентов составляет значение одного числа от другого.Подводя итоги, можно сказать, что калькулятор позволяет определиться с такими вопросами:

1. Вычислить определенный % из определенного значения. Или, если известен %, то прибавить его к какому-то числу.
2. Какой % составляет от заданного показателя.
3. Сколько % содержит одно значение от другого.

На обычном калькуляторе также есть функция определения %. Если опция есть, то должна быть клавиша, где изображен %.

Для этого найдите на его клавиатуре кнопку с изображением процента (%).

Для этого проведем следующие манипуляции:

Введите 125 на калькуляторе. Нажмите умножить (*). Нажмите 12. Затем нажмите кнопку с процентом. При этом на экране отобразиться результат – 9,6%.

Таким образом, можно найти любые другие значения с двумя числами. Калькулятором можно и воспользоваться на мобильном телефоне.

В ноутбуке или компьютере полезную программку можно отыскать через меню пуск.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Как решаем:

76 : 100 = 0,76 — 1% от массы человека

0,76 * 70 = 53,2

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Как решаем:

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

х – 0,4х = 0,6x

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х – 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

х – 0,45x = 0,55х

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Ответ: 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

Как решаем:

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

100 – 8 = 92

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

92 : 4 = 23

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

23 * 5 = 115

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

Как решаем:

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Как решаем:

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.

19 : 0,1 = 190

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 – 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Как вычесть процент от суммы без помощи калькулятора

Если же требуется от уже известной суммы отнять неизвестное число, составляющее какое-то количество процентов, можно воспользоваться следующими методами:

1. Вычислить неизвестное число с помощью одного из приведенных выше способов, после чего отнять его от исходного.
2. Сразу рассчитать остающуюся сумму. Для этого от 100% отнимаем то число процентов, которое нужно вычесть, и полученный результат переводим из процентов в число любым из описанных выше способов.

Второй пример удобнее, поэтому проиллюстрируем его. Допустим, надо узнать, сколько останется, если от 4779 отнять 16%. Расчет будет таким:

1. Отнимаем от 100 (общее количество процентов) 16. Получаем 84.
2. Считаем, сколько составит 84% от 4779. Получаем 4014,36.

Примеры задач

Как рассчитать стоимость кредита

Если вы хотите приблизительно знать, во сколько вам обойдётся банковский кредит, который вы берёте, вот вам простая формула:

полная стоимость кредита=сумма кредита×

Эта формула, как вы понимаете, не учитывает комиссий, платы за обслуживание кредита, страховых взносов, штрафов за просрочку, пени и прочих расходов. Но вы всё равно можете ею пользоваться, чтобы грубо оценить полную стоимость вашего кредита.

Задача. Вы хотите взять 10 млн рублей в ипотеку под 10 % годовых на срок 15 лет (допустим, первый взнос вы уже внесли). Во сколько вам обойдётся данный кредит?

Решение. Полная стоимость кредита составит 10 млн × (1+0,01×10×15)=10 млн × 2,5=25 млн рублей, то есть вам придётся заплатить общую сумму в 25 млн рублей, в которую, помимо суммы долга в 10 млн рублей, входит сумма процентов за пользование кредитом, равная 25–10=15 млн рублей, или 1 млн рублей в год.

Как рассчитать сумму комиссии

Часто нам приходится оплачивать мобильную связь, пополнять электронные кошельки, совершать те или иные платежи. Во всех случаях присутствует тот или иной процент комиссий за пользование сервисом. Как быть, если вы хотите точно знать, какая сумма ляжет вам на счёт или на баланс, или же спишется с вашего электронного кошелька в результате комиссий? Ответ прост. Используйте калькулятор или ваш ум, а также приведённую выше инструкцию вместе со следующей формулой:

сумма с учётом комиссии=требуемая сумма× + фиксированная комиссия

Задача. Какая сумма спишется с баланса мобильного при пополнении с него электронного кошелька, если вы хотите положить на кошелёк 100 рублей, причём комиссионный процент равен 8 %, а фиксированная комиссия составляет 10 рублей?

Решение. Сумма с учётом комиссии будет равна 100×(1+0,01×8)+10=100×1,08+10=118 рублей. Именно такую сумму нужно указать в платежной форме, чтобы у вас на кошельке появились 100 рублей.

Рентабельность вашего бизнеса

Как рассчитать эффективность вашего бизнеса? Для этого нужно знать обобщённые показатели деятельности фирмы, которой вы руководите, такие, как валовая прибыль за прошедший период (который может составлять месяц, квартал, полугодие, год) и общие затраты за тот же период. Тогда вы сможете найти рентабельность вашей деятельности, которая показывает чистую прибыль на 1 рубль затрат:

рентабельность=[(валовая прибыль – общие затраты)/общие затраты]×100 %

Задача. Валовая прибыль вашего бизнеса за прошедший год составила 10 млн рублей при общих затратах в 8 млн рублей. Чему равна рентабельность бизнеса за прошедший год?

Решение. Рентабельность бизнеса равна [(10 млн – 8 млн)/8 млн]×100 %=0,25×100 %=25 %, т. е. на каждый вложенный рубль вы получили доход в 25 копеек.

На сколько % перевыполнен план

Если нужно узнать, насколько величина А больше величины В в процентном отношении, то пригодится следующая формула:

увеличение (прирост) А по сравнению с В=[(А – В)/В]×100 %

Задача. Завод запланировал в текущем квартале выпуск 300 тыс. подшипников, но фактически было произведено 420 тыс. подшипников. На сколько процентов был перевыполнен план по выпуску изделий?

Решение. План за квартал был перевыполнен на [(420 тыс. – 300 тыс.)/300 тыс.]×100 %=

=0,4×100 %=40 %.

На сколько % упала прибыль

Когда вы хотите знать, на сколько величина А меньше величины В в процентном отношении, воспользуйтесь следующей формулой:

уменьшение А по сравнению с В=[(В – А)/В]×100 %

Задача. Прибыль вашего предприятия за последний месяц снизилась со 100 тыс. рублей до 90 тыс. рублей. На сколько процентов упала прибыль за прошедший месяц?

Решение. Снижение прибыли составило [(100 тыс. – 90 тыс.)/100 тыс.]×100 %=10 %.

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит 2,5 * 15 = 37,5 — это 15%. 250 – 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Как использовать калькулятор процентов

Кроме обычного соотношения чисел и их процентного эквивалента, с помощью калькулятора можно провести простые математические вычисления увеличения или уменьшения заданного числа на количество процентов. Для этого достаточно заполнить соответствующие поля и нажать на кнопку “Рассчитать”.

Например, чтобы узнать сколько составит 5% от числа 80, ставим значения внужные поля. После нажатия кнопки расчета получим результат “4”.

Точно также калькулятор посчитает в каком процентном соотношении находятся два разных числа. Например 80 к 100 составит 80%.

С помощью калькулятора можно

• прибавить % — если к числу 80 прибавить 5%, то получим 84;
• вычесть % — если от числа 80 вычесть 5%, то получим 76.

Такие вычисления нужны, как для работы, так и в обычной жизни.

1. В магазине, когда мы видим на ценнике скидку 35%, калькулятор поможет быстро посчитать, какую сумму фактически надо заплатить.
2. На кухне, когда готовим блюдо, часто надо делать пересчет при изменении количества порций.
3. На работе, например в магазине, когда надо проанализировать соотношение выручки от нескольких продавцов, чтобы оценить качество работы. Также понадобится подсчет процентов для определения нагрузки, допустим почасовой, еженедельной и т.д.
4. Когда есть необходимость получения кредита. Вычисление суммы, которую включает процентная ставка, поможет подобрать наиболее выгодный вариант. То же касается и депозитов.
5. Не обойтись без процентов и копирайтерам. Любой заказчик хочет получить 100% уникальность при низком спаме и водности текста.

Способ четвёртый: составляем пропорцию

Посчитать процент от суммы можно с помощью составления пропорции. Это ещё одно страшное слово из школьного курса математики. Пропорция – равенство между двумя отношениями четырёх величин. Для наглядности лучше сразу разобраться на конкретном примере. Вы хотите купить сапоги за 8 000 рублей. На ценнике указано, что они продаются со скидкой 25%. Сколько же это в рублях? Из 4 величин мы знаем 3. Есть сумма 8 000, которая приравнивается к 100%, и 25%, которые требуется посчитать. В математике обычно неизвестную величину называют X. Получается пропорция:

8000 – 100%

X –  25%

Для удобства подсчётов переводим проценты в десятичные дроби. Получаем:

8 000 – 1

X – 0,25

Решается пропорция так: Х = 8 000 * 0,25 : 1X = 2 000

2 000 рублей – скидка на сапоги. Вычитаем эту сумму из старой цены. 8 000 – 2 000= 6 000 рублей (новая цена со скидкой). Вот такая приятная пропорция.

Этим методом можно воспользоваться и для определения значения 100%, если знаете числовой показатель – допустим, 70%. На общекорпоративном собрании шеф объявил, что за год было продано 46 900 единиц товара, при этом план выполнен лишь на 70%. Сколько же необходимо было продать, чтобы выполнить план полностью? Составляем пропорцию:

100% – Х

70%  – 46 900

Переводим проценты в десятичные дроби, получается:

1 – Х

0,7 – 46 900

Решаем пропорцию: Х = 46 900 * 1 : 0,7Х = 67 000. Вот таких результатов работы ожидало начальство.

Как вы уже догадались, методом пропорции можно вычислить, сколько процентов составляет числовой показатель от суммы. Например, выполняя тест, вы ответили правильно на 132 вопроса из 150. Сколько процентов задания было сделано?

150 – 100%

132 – Х%

Переводить в десятичные дроби эту пропорцию не надо, можно сразу решать.

Х = 100 * 132 : 150. В итоге Х = 88%

Как видите, не так уж всё и страшно. Немного терпения и внимания, и вот уже вычисление процентов вами осилено.

Считаем соотношения

Чтобы перевести проценты в обычное число, иногда можно использовать дроби. Например, 5% — это 1\20 числа. То есть, от 100 это будет 5.

Вот самые распространенные соотношения:

• 20% — 1\5, делим число на 5;
• 25% — 1\4, делим на 4;
• 50% — 1\2;
• 10% — 1\10;
• 5% — 1\20;
• 75% — 3\4.

В таких соотношениях сначала нужно разделить на 4, а затем умножить на 3.

Например, вы нашли в магазине вещь, которая стоит 3500. Однако, консультант говорит, что сейчас действует акция на все вещи – скидка 30%.

Вам надо посчитать новую стоимость товара.

Итак: 100%-30% = 70% — стоимость в процентах от первоначальной цены после скидки.

Новая цена составляет 2100.

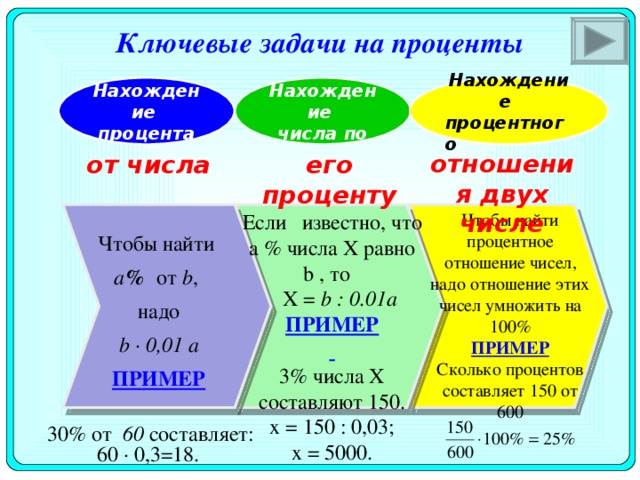
Три типа задач на проценты

Для всех видов практических задач на проценты используется универсальная формула:

p=(A/B)x100%;

где р — процент, который число А составляет от числа В. (1).

Величину р следует трактовать здесь как количество сотых долей, которые число, А составляет от числа В. Пользуясь этой формулой, можно решать три типа задач, по числу неизвестных в ней.

Задачи первого типа

Здесь необходимо найти неизвестное число процентов. Для этого используется формула (1). Вот простейший пример: сколько % от 25 составляет число 12,5?

Решение: p=(12,5/25)x100%=50%.

Задачи второго типа

Нужно найти, сколько будет р % от числа В. Из (1) можно легко получить следующую формулу:

А=(р/100)xВ. (2).

Задача. Сколько будет 13% от 6700 рублей?

Решение: А=(13/100)x6700=871 рубль.

Задачи третьего типа

Если известно, что р % от числа В равно А. Чему равно В? Из (1) следует, что

В=(100xА)/р. (3).

Задача. 7% от некоторого числа равно 777. Чему равно само число?

Решение: В=(100×777)/7=11100.

Проценты: правила

Рассмотрим четыре известных способа поиска процентов.

Занимайтесь математикой в удовольствие вместе с нашими преподавателями на курсах по математике для учеников с 1 по 11 классы!

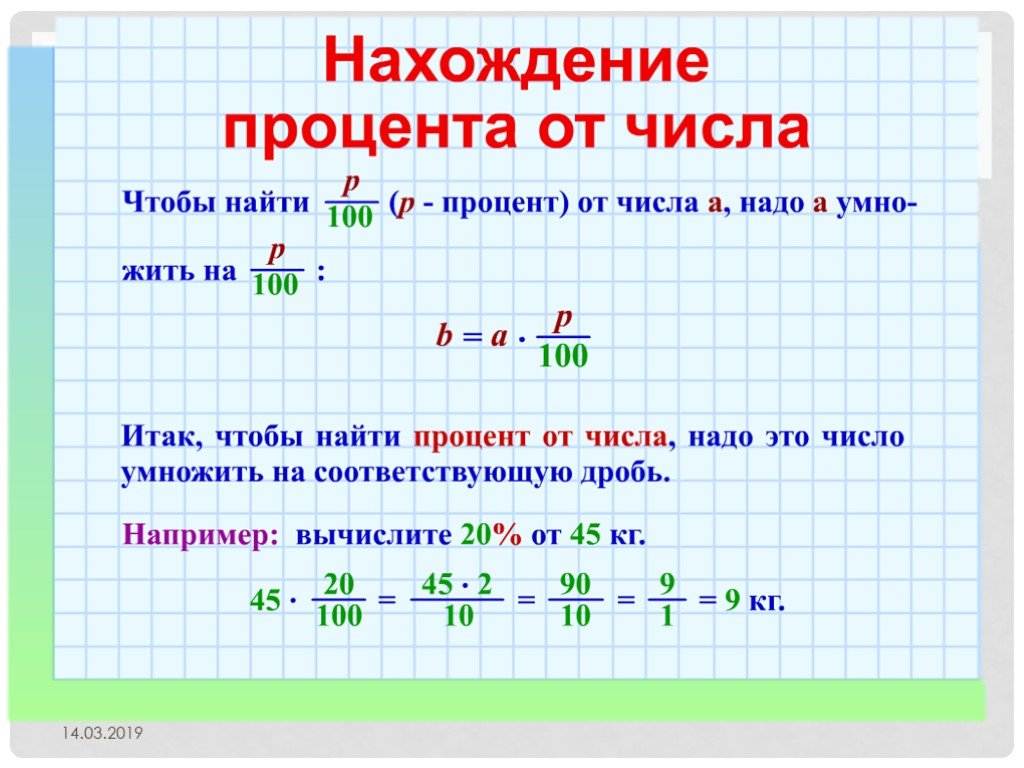
Нахождение одного процента от числа

При делении на 100% получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать проценты от суммы, нужно умножить их на величину 1%. А чтобы перевести известное значение в проценты, следует разделить его на величину 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит, 2,5 × 15 = 37,5 — это 15%. 250 – 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой. 

С помощью метода пропорции можно рассчитать любые проценты. Выглядит это так:

a : b = c : d. 

Читается: а относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию: 1390 руб. = 100% x руб. = 14% Перемножим крест-накрест и найдем x: x = 1390 × 14 : 100 x = 194,6

Ответ: выгода по скидке составила 194,6 рубля.

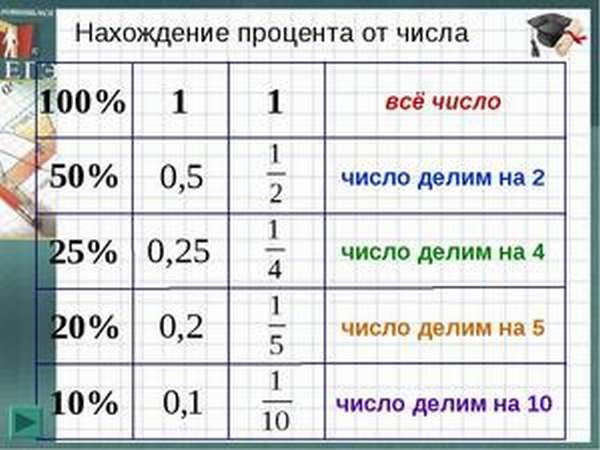
Соотношения чисел

Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.

Процент	Дробь	Как найти % от числа a
10%	1/10	a : 10
20%	1/5	a : 5
25%	1/4	a : 4
50%	1/2	a : 2
75%	3/4	a : 4 × 3

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100% – 25% = 75%, значит, нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 75% — это 3/4 от числа, значит, 8500 : 4 × 3 = 6375 (рублей).

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

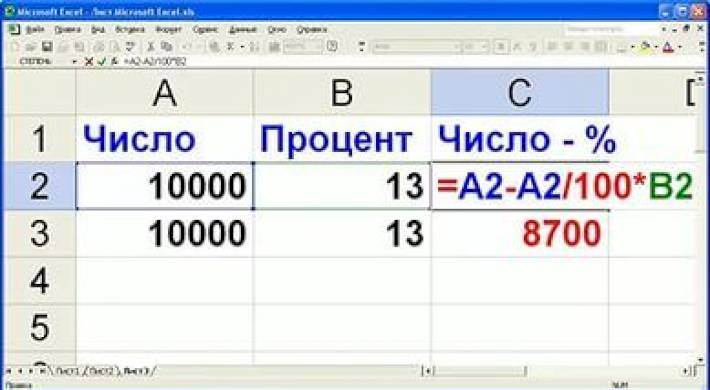
Расчет процентов в Excel.

Основная формула для расчета процента от числа в Excel такая же, как и во всех сферах жизни:

Часть / Целое = Процент

Если вы сравните ее с основной математической формулой для процента, которую мы указали чуть выше, то  заметите, что в формуле процента в Excel отсутствует часть * 100. При вычислении процента в Excel вам совершенно не обязательно умножать полученную дробь на 100, поскольку программа делает это автоматически, когда процентный формат применяется к ячейке.

И если в Экселе вы будете вводить формулу с процентами, то можно не переводить в уме проценты в десятичные дроби и не делить величину процента на 100. Просто укажите число со знаком %.

То есть, вместо =A1*0,25   или =A1*25/100 просто запишите формулу процентов  =A1*25%.

Хотя с точки зрения математики все 3 варианта возможны и все они дадут верный результат.

А теперь давайте посмотрим, как можно использовать формулу процента в Excel для реальных данных. Предположим, в вашей таблице Эксель записана сумма заказанных товаров в столбце F и оставленных товаров в столбце G. Чтобы высчитать процент доставленных товаров, выполните следующие действия:

• Введите формулу =G2/F2 в ячейку H2 и скопируйте ее на столько строк вниз, сколько вам нужно.
• Нажмите кнопку «Процентный стиль» ( меню «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в виде процентов.
• Не забудьте при необходимости увеличить количество десятичных знаков в полученном результате.
• Готово! 🙂

Такая же последовательность шагов должна быть выполнена при использовании любой другой формулы процентов в Excel.

На скриншоте ниже вы видите округленный процент доставленных товаров без десятичных знаков.

Чтобы определить процент доставки, мы сумму доставленных товаров делим на сумму заказов. И используем в ячейке процентный формат, при необходимости показываем десятичные знаки.

Запишите формулу в самую верхнюю ячейку столбца с расчетами, а затем протащите маркер автозаполнения вниз по столбцу. Таким образом, мы посчитали процент во всём столбце.

Онлайн-калькулятор

Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета процента от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть проценты: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

Если на уроке в 5 или 6 классе вам нужно проверить правильность нахождения процента от числа, то поможет онлайн-калькулятор. Вот несколько сайтов, к которым можно обратиться:

• раз,
• два,
• три,
• четыре.

Как посчитать, сколько это процентов?

Этот вопрос задает каждый покупатель магазина, который намеревается воспользоваться акцией, и каждый сотрудник компании, желающий узнать размер своего вознаграждения за выполнение плана. Ведь проценты присутствуют во многих сферах повседневной жизни.

Возьмем конкретный пример. В магазине наушники стоили 3000 рублей, на них появилась акция в виде скидки 30%. Какая сумма вашей выгоды и сколько надо заплатить за товар?

Расчет простой

• 3000×30/100 = 900, поскольку 30/100 можно еще записать как 0,30, то
• 3000×0,30 = 900 рублей — это сумма скидки (30%) в денежном эквиваленте.

Теперь посчитаем сколько надо заплатить за наушники: 3000-900=2100 руб.

Расчет процентов — это не только задание на уроке в школе, но и актуальный вопрос для многих взрослых. Не у всех есть способность быстро выполнять действия в уме. Хотя рассчитать 10% или 20% от заданной суммы довольно просто, вычисление размера, например процентной ставки по банковским операциям иногда бывает проблематичным.

Что делать в этой ситуации? Вы можете прибегнуть к помощи специалиста, но проще применить свои навыки в использовании современных технологий и использовать онлайн калькулятор расчета процентов.

О легких и простых методах расчета процентов вы узнаете из видео.

Читайте далее:

Калькулятор автокредита: рассчитать процент переплаты

Онлайн конвертер долей, перевод дюжин, процентов, промилле и других единиц

Особенности ипотечного кредита: что нужно знать перед оформлением

Калькулятор сравнения шин, преимущества и недостатки изменения размера

Калькулятор расхода топлива, как рассчитать стоимость поездки

Онлайн калькулятор расчета времени зарядки АКБ (постоянным током), сколько заряжать аккумулятор

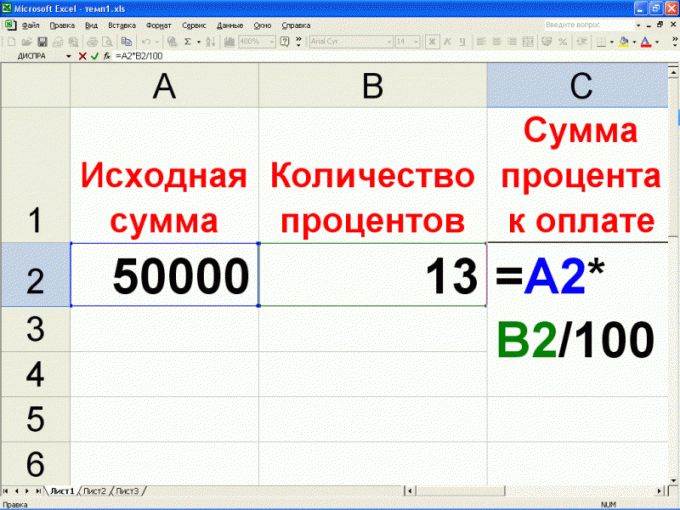
Как считать проценты в excel?

Если у вас под рукой имеется компьютер или ноутбук с операционной системой Windows, вам не составит большого труда подсчитать процент от необходимой суммы. Приведем для этого простой пример.

Нам необходимо найти 8% от 358.

1. Открываем Excel.
2. Находим свободную строку.
3. Вводим данные.
4. Ставим знак «=» и делаем подсчет.
5. Получаем 28,64.

Аналогично к подсчетам на калькуляторе, вы можете ввести в Excel знак %, и это тоже будет правильно.

Иногда нам необходимо узнать процентный показатель от суммы.

1. К примеру, у нас есть список сотрудников и сумма, на которую они произвели продаж. Помимо этого, известна сумма возвратов. По этим данным мы рассчитываем процент возвратов по товарам.
2. Просчитаем процент для первого показателя в списке — процент возвратов некоего Петрова.
3. Для начала составляем пропорцию, где 100% — это 35682(сумма продаж Петрова). х% — 2023 (сумма возвратов Петрова).
4. Решаем эту пропорцию по формуле, известной нам со школы.
5. Прописываем формулу в ячейке D2 и спускаемся немного вниз =C2*100%/B2.
6. К ячейке, в которой высветился результат, применяем формат «Процентный». Выделяем ячейки, правой кнопкой жмем на любой из них и выбираем «Формат». Во вкладке «Число» выбираем «Процентный». Система автоматически пропишет значок %.

7. Применив нашу формулу ко всем данным, получаем результат.

Расчет доли в процентах (удельного веса).

Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.

Пример 1. Сумма находится в конце таблицы в определенной ячейке.

Очень распространенный сценарий – это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.

Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы: 

=G2/$G$13

Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.

Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.

На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.

Пример 2. Часть итоговой суммы находится в нескольких строках.

В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.

В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:

Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:

Естественно, вы можете указать название товара прямо в формуле, например:

Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.

Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:

Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.

Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:

• Как использовать функцию СУММЕСЛИ в Excel
• СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями

Простые и сложные %

Рассмотрим ещё тип задач, относящихся к финансовым и связанных с процентами. Это такие задачи, в которых нужно вычислять доход от вклада или инвестиций. Вот такой пример. Вы вложили деньги в банк под р % годовых некую сумму S0. Чему будет равен ваш капитал через n лет? И ответ на этот вопрос зависит от того, какой у вас вклад: с простым начислением процентов или с их капитализацией.

Простое начисление процентов — это ежегодное (ежеквартальное, ежемесячное) получение р % от суммы вашего вклада, когда начальная сумма вклада S0 фиксирована, а вы регулярно с этой суммы получаете фиксированный доход, то есть каждый год (квартал, месяц) вы получаете прибыль 0,01p•S0. Через n лет ваша прибыль станет равна 0,01nр•S0. Полученная прибыль суммируется с вашим начальным вкладом S0, в результате чего вся сумма прибыли вместе с процентами составит:

S=S0•(1+0,01np). (4).

Задача. Вы положили 100000 рублей в банк под 10% годовых на 5 лет. Чему станет равен ваш вклад?

Решение: S=100000•(1+0,01•5•10)=100000•1,5=150000 рублей.

Допустим теперь, что ваш вклад с капитализацией процентов. Это означает, что после каждого начисления проценты прибавляются к уже имеющейся сумме на вашем счету. Таким образом, после следующего начисления сумма процентов становится больше. Например, в первый год проценты по вкладу с капитализацией составят 0,01р•S0, а за второй год эта сумма будет уже больше и составит 0,01p•(S0+0,01p•S0)=0,01p•S0•(1+0,01р), а за третий год — 0,01p•(S0+0,01p•S0•(1+0,01р))=0,01р•S0•(1+0,01p+(0,01p)²).

Выражение в скобках представляет собой сумму геометрической прогрессии, которая равна (0,01р)². Поэтому за третий год сумма на вашем счету станет равной S0+S0•(0,01р)³. Продолжая так дальше, через n лет или периодов начисления, сумма на счету вместе с начисленными процентами составит:

S=S0•(1+0,01р)ⁿ. (5).

Мы получили так называемую формулу сложных процентов, которая позволяет высчитывать сумму на вашем счету по вкладу с капитализацией процентов.

Задача. Вы положили всё те же 100 000 рублей на 5 лет под 10 % годовых, но открыли вклад с капитализацией. Сколько к концу указанного срока будет на вашем счету?

Решение. Пользуясь формулой сложных процентов, получим: S=100000•(1+0,01•10)^5=100000•1,1^5=100000•1,61051=161051 рубль.

Сравнивая результаты, полученные по формулам (4) и (5), видим, что по вкладу с капитализацией сумма на счету стала больше на 11051 рубль по сравнению с обычным вкладом, где происходит простое начисление процентов. Таким образом, второй способ вложения денег выгоднее.