Произвольный треугольник
Фигура с тремя углами является самым простым замкнутым объектом в геометрии. В общеобразовательных школах ее изучению уделяют наибольшее время, поскольку многие основные геометрические свойства заложены именно в ней. Построить ее несложно, для этого необходимо взять три точки на плоскости так, чтобы они не располагались на одной прямой. После этого следует попарно соединить их прямыми отрезками.
Треугольник произвольного типа состоит из следующих элементов:

- три вершины;
- три стороны, которые в общем случае имеют различную длину;
- одна вершина в совокупности с парой прилегающих к ней сторон образует угол, их в треугольнике три.
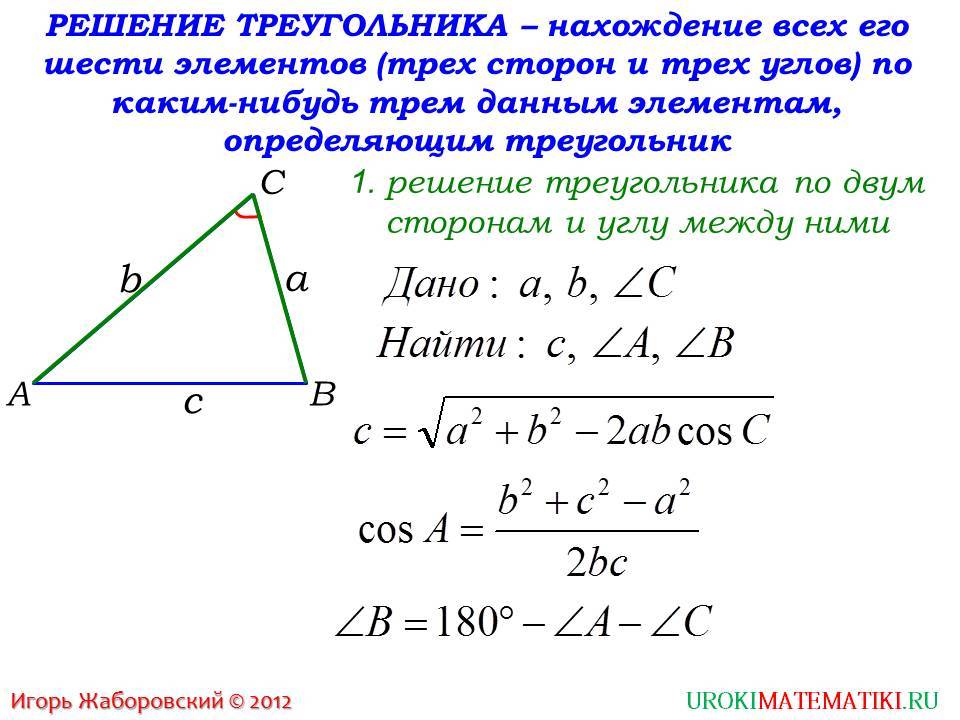
Для рассматриваемой фигуры всегда справедливы три важных математических соотношения между ее длинами сторон и углами. Эти соотношения часто используют для решения разнообразных задач. К ним относятся следующие:
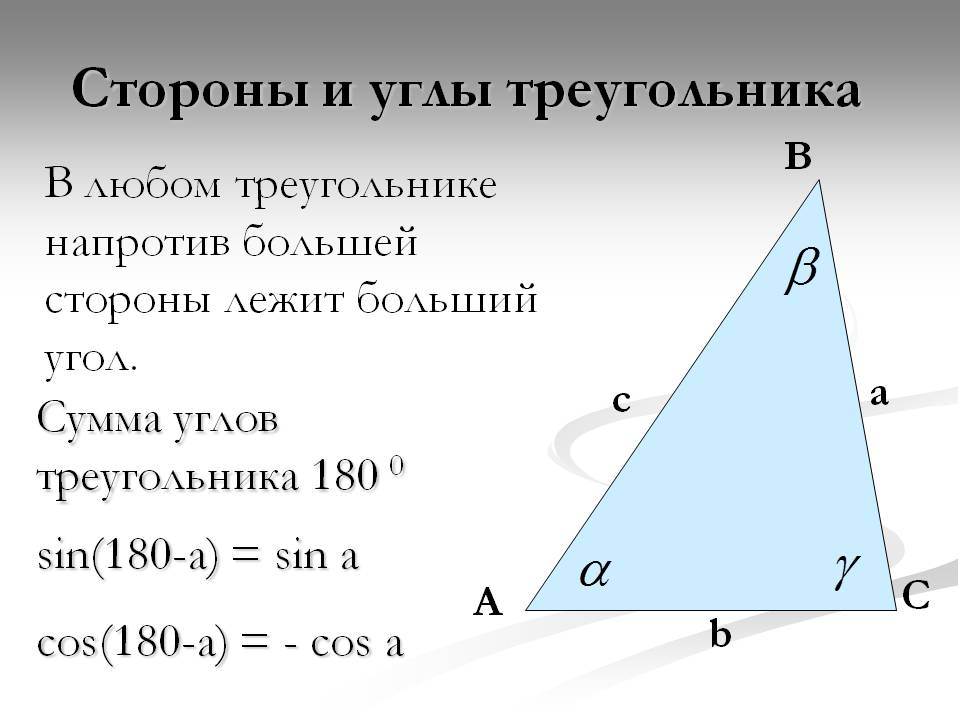
- О сумме углов. Треугольник характеризуется тремя углами, сумма которых всегда составляет 180 градусов или пи радиан. Это свойство следует из характеристики евклидовой геометрии на плоскости. Его записывают так: ∠ A + ∠ B + ∠ C = 180 °, где символом ∠ обозначен угол при соответствующей вершине.
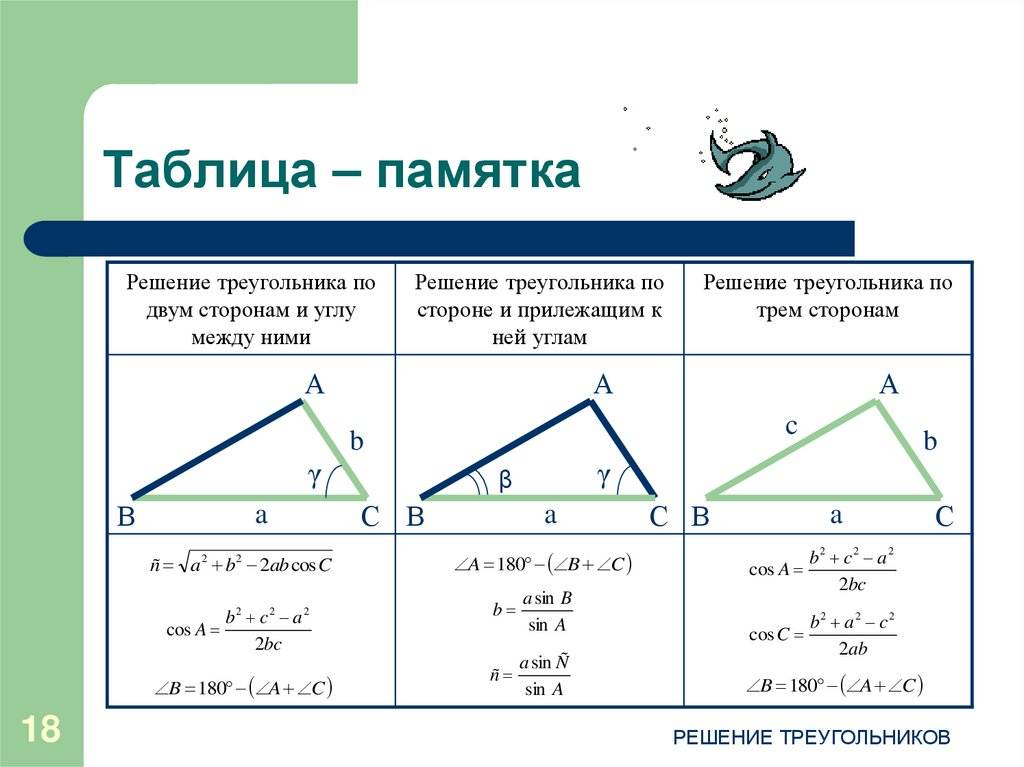
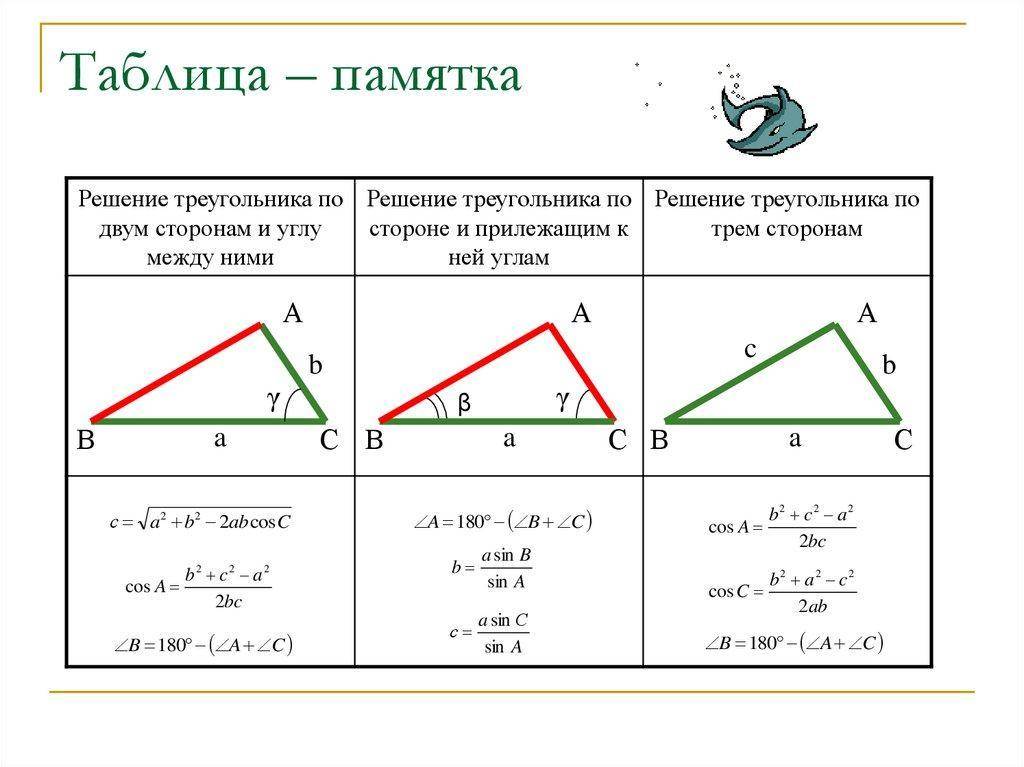
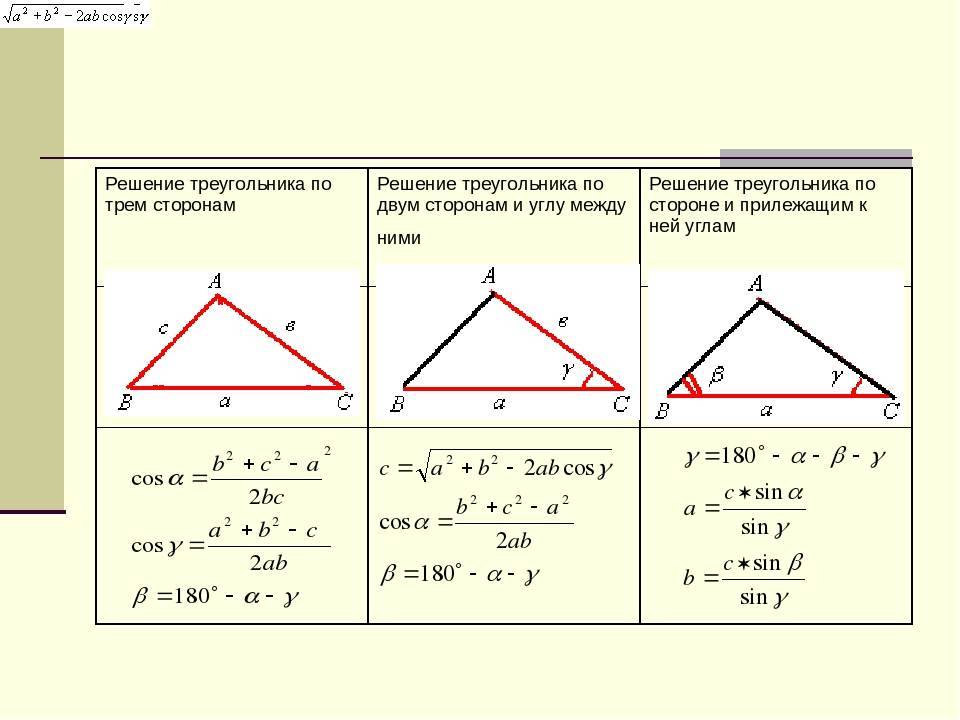
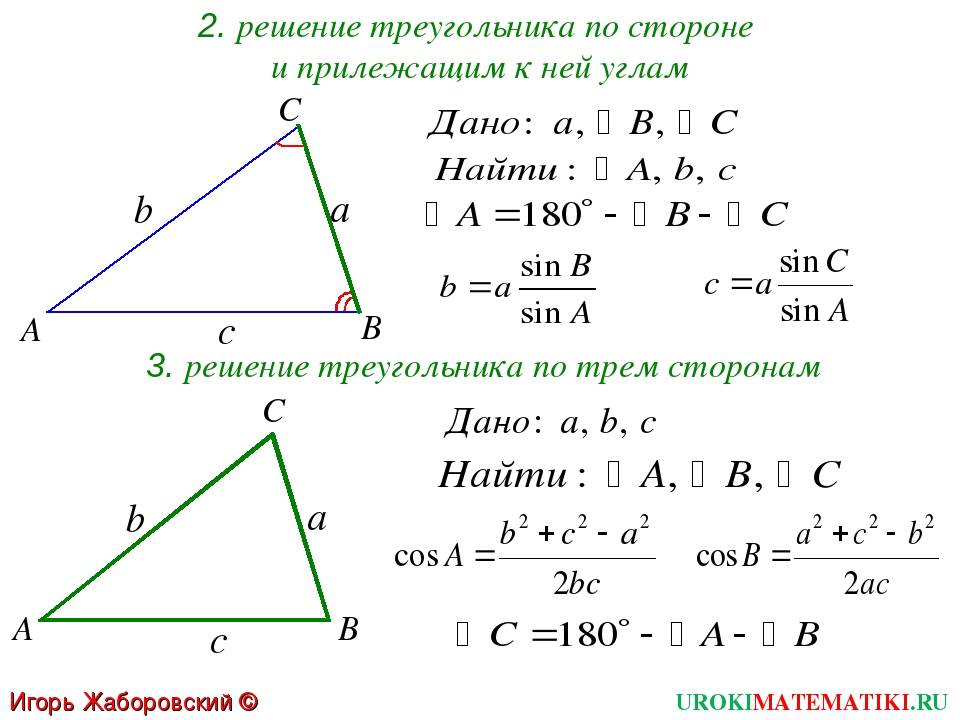
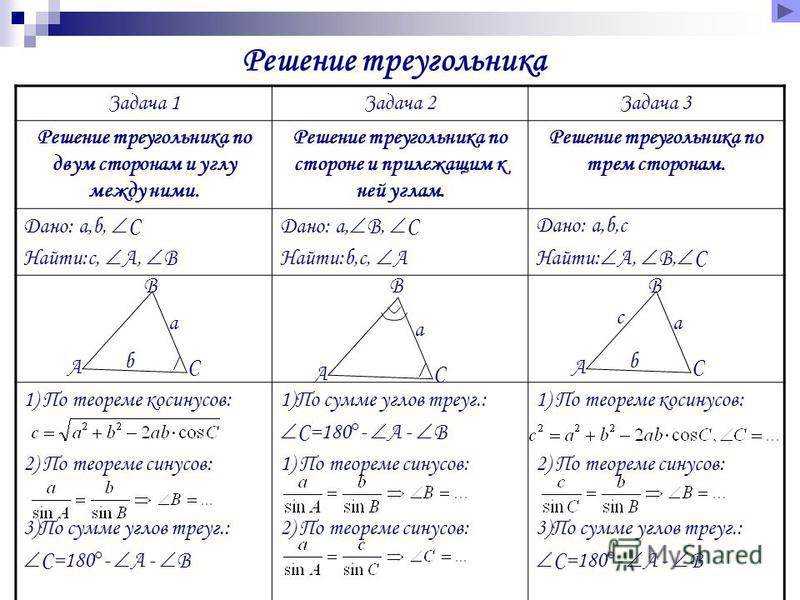
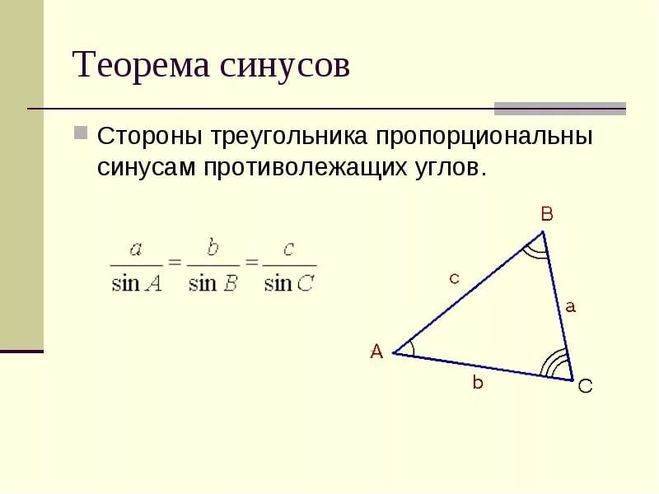
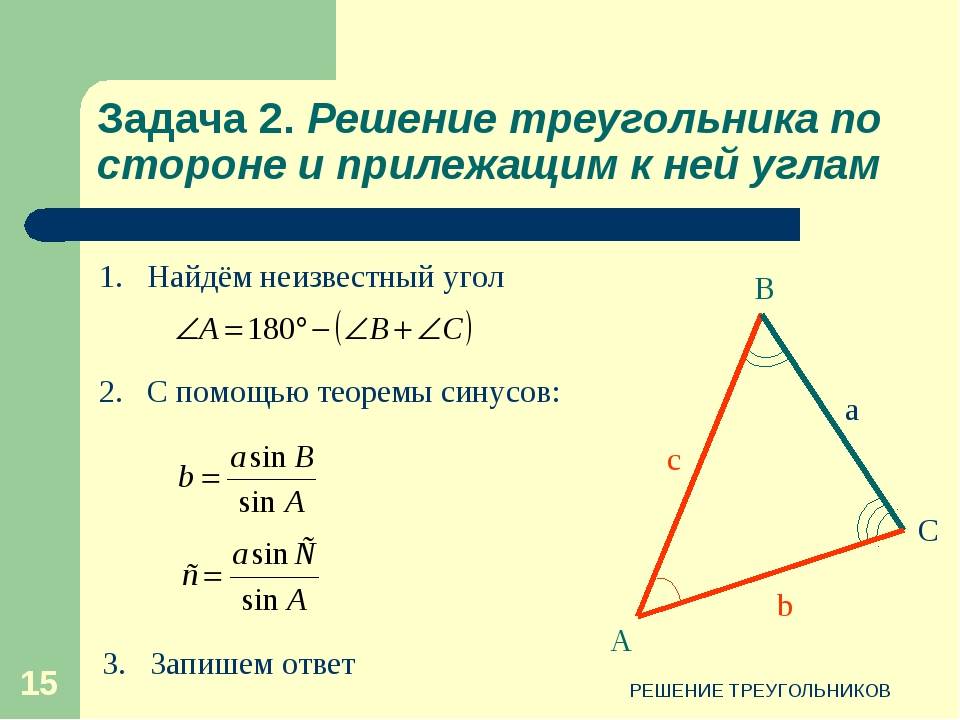
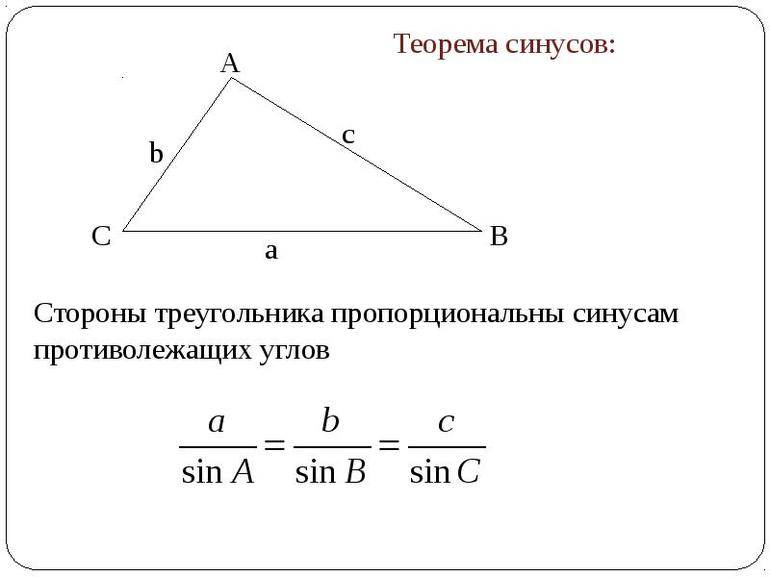
- Теорема синусов. Словесная ее формулировка следующая: отношение длины стороны треугольника к синусу лежащего напротив нее угла является величиной постоянной для данной фигуры. Математически это утверждение записывается так: a/sinA = b/sinB = c/sinC, где буквами a, b и c обозначены длины сторон треугольника. Это выражение удобно использовать, когда по условию задачи известна одна сторона и два угла, и необходимо найти оставшиеся элементы фигуры.
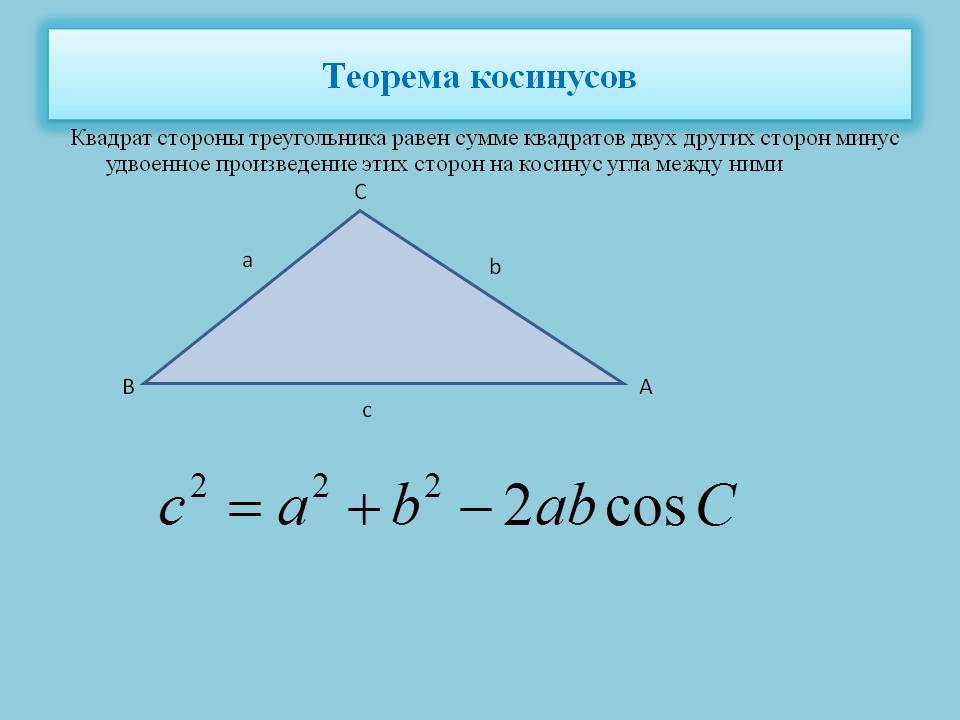
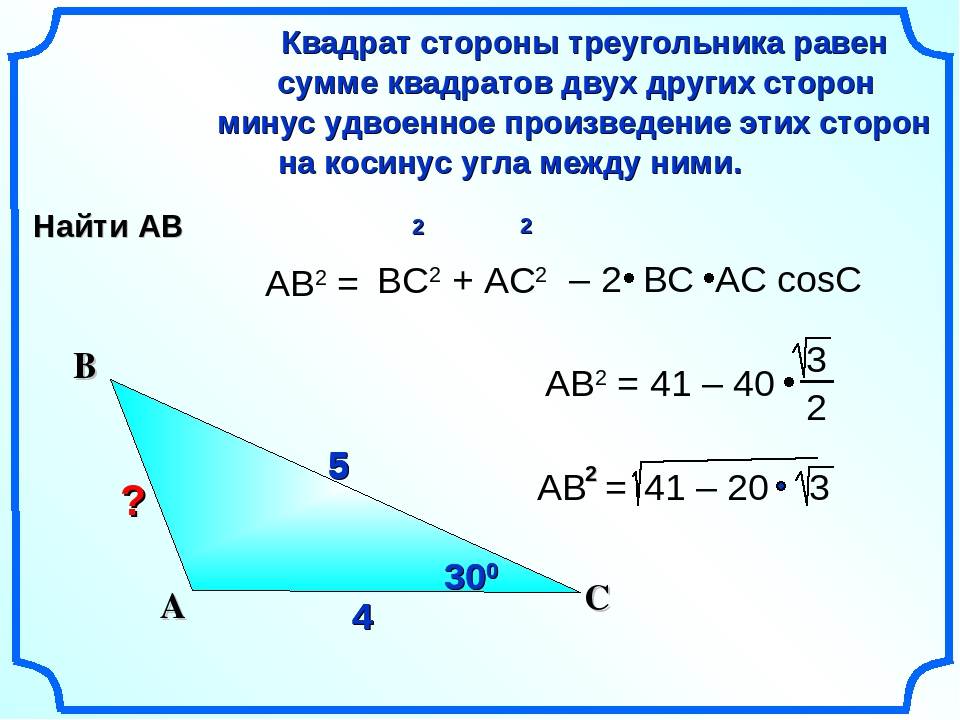
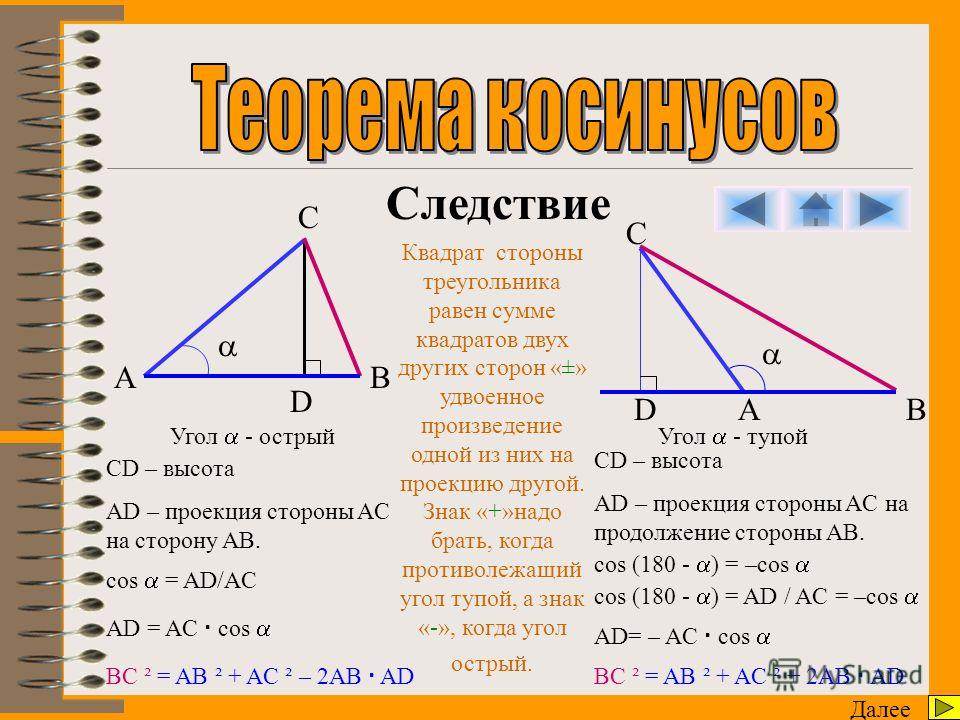
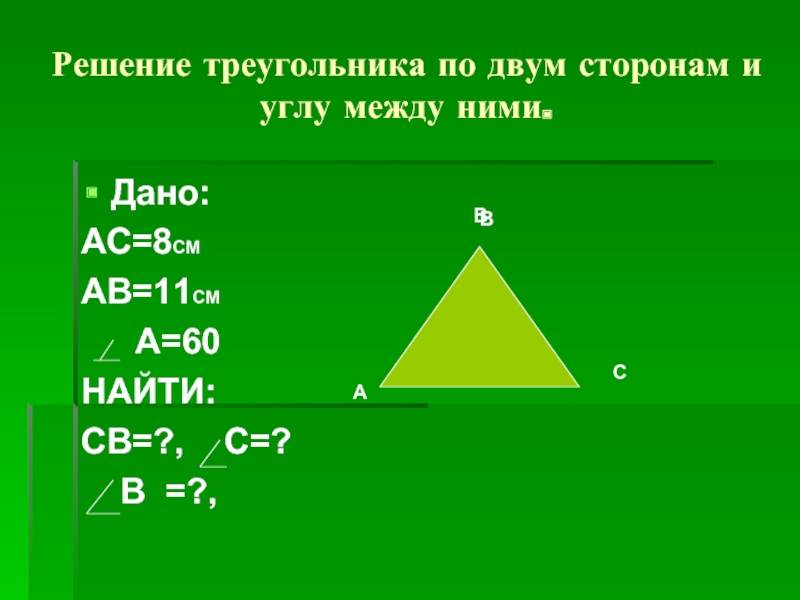
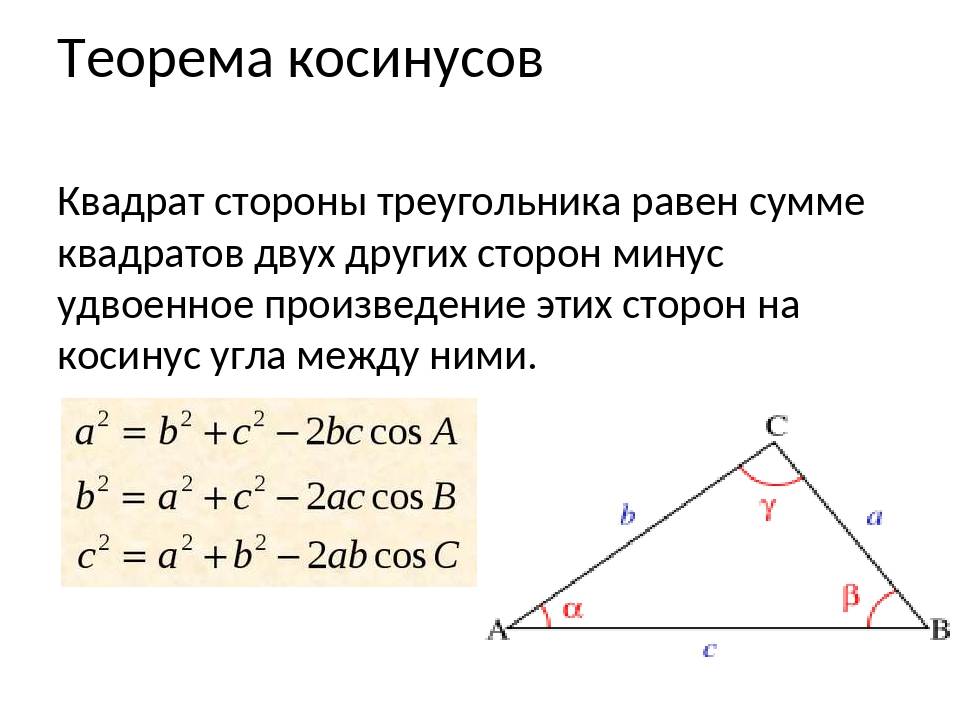
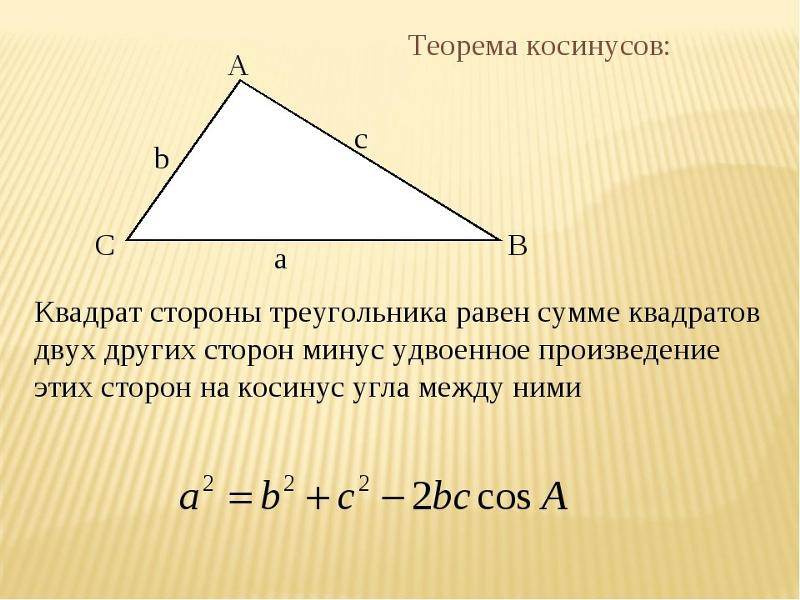
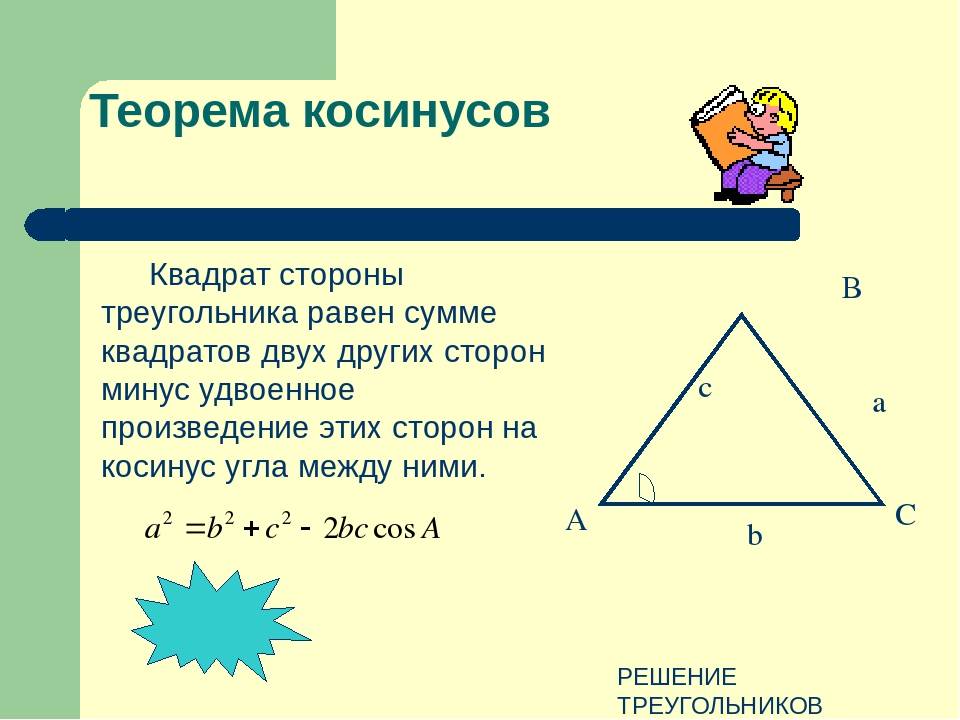
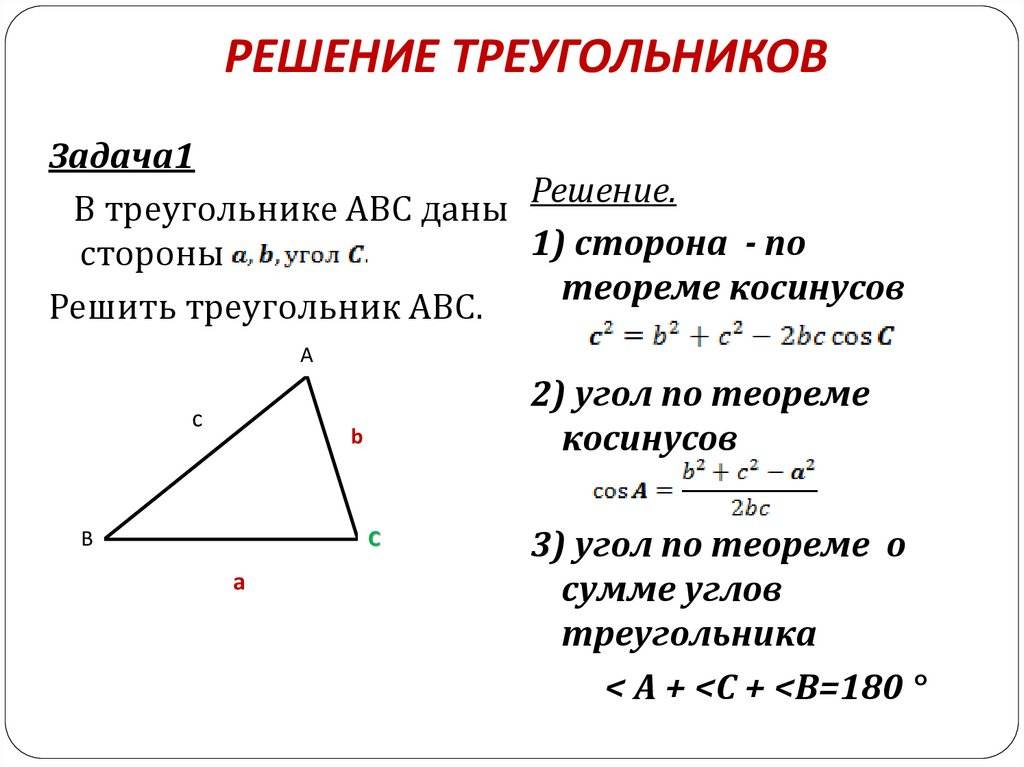
- Косинусов теорема. Она звучит так: квадрат стороны треугольника равен сумме квадратов двух оставшихся сторон за вычетом их удвоенного произведения, которое помножено на косинус угла между ними. Несмотря на несколько громоздкую формулировку, теорема имеет лаконичную математическую формулу: c 2 = a 2 + b 2 — 2*a*b*cosC. Это выражение удобно применять, когда известны две стороны и угол в треугольнике.
Как найти сторону треугольника — в помощь школьнику :
Есть несколько способов решения этой геометрической задачи. Они описаны в статье.
При помощи сторон и углов
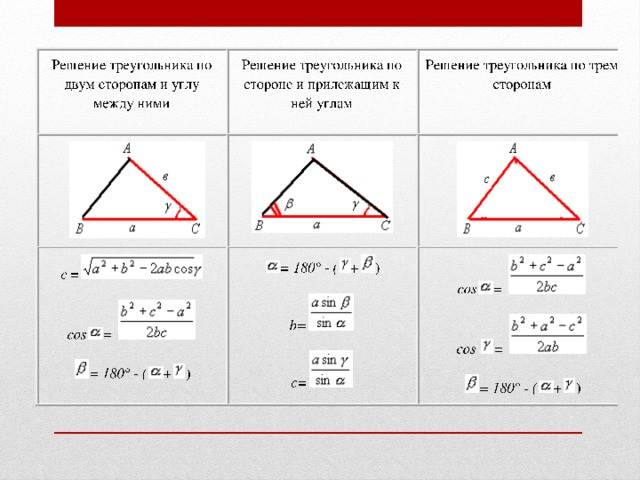
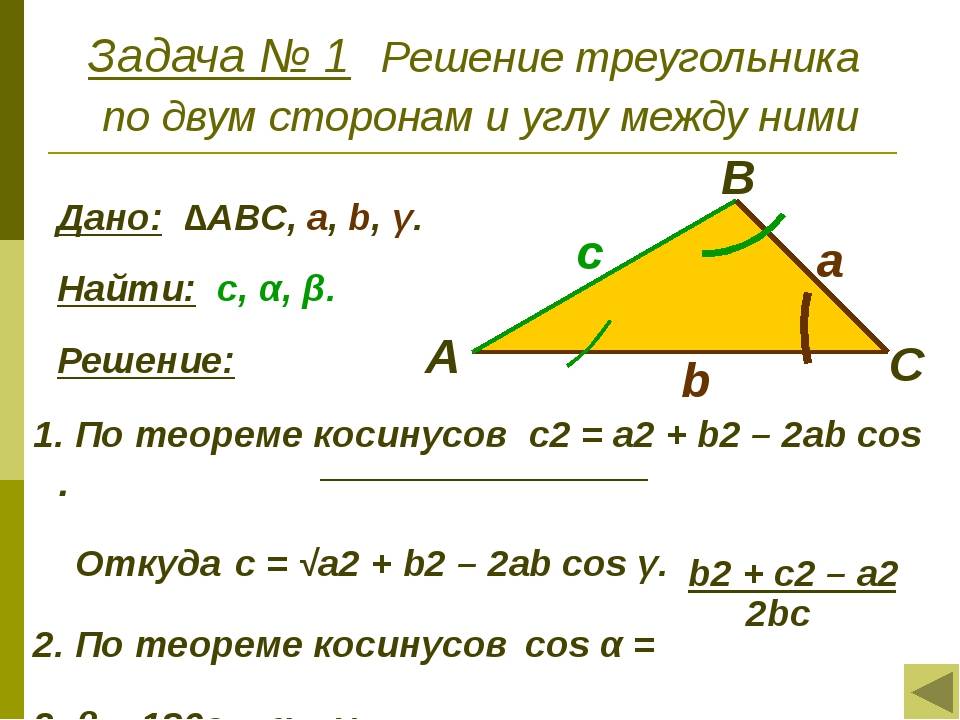
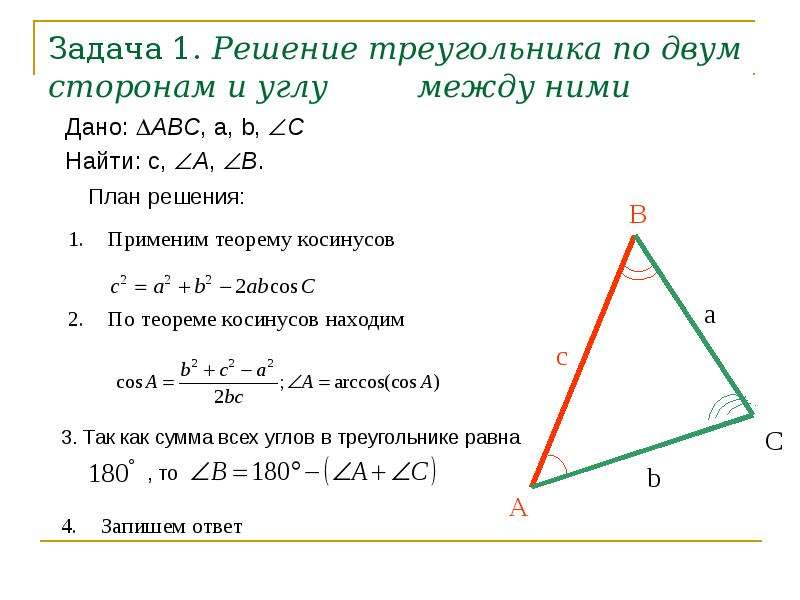
Итак, первый способ нахождения сторон треугольника — это по нескольким сторонам и углу между ними (и аналогично с углами и одной прилежащей стороной). Данный способ подойдет для старшей школы, так как здесь используются такие понятия, как синус, косинус, квадрат числа и корень.
Итак, как найти сторону треугольника, который является произвольным? Для начала нарисуем эту самую фигуру. Теперь давайте обзовем элементы нашей фигуры. Стороны будут a, b и c. Угол, находящийся напротив стороны a, у нас будет «альфа», напротив b -«бета», напротив c — «гамма».
Для того чтобы найти сторону, скажем, a, необходимо вычислить квадратный корень из суммы квадрата b, c и вычесть из нее двойное произведение косинуса угла a на стороны b и c. То есть, для того, чтобы облегчить вид формулы и пояснить, как найти сторону треугольника произвольной формы, можем написать следующее: a=(b*b+c*c-2*b*c*cos»альфа»)^(1/2).
Тогда, опираясь на обозначения, получим следующее: a=(b*sin»альфа»)/sin»бета»=(b*sin»альфа»)/sin(«альфа»+»гамма»)=(b*sin(«бета»+»гамма»))/sin»бета». Вот таким мудреным способом можно найти неизвестную сторону произвольного треугольника.
Равнобедренный треугольник
Что такое равнобедренный треугольник? Сам по себе он имеет две одинаковые стороны и так называемое основание. Стороны-близнецы обозначим буквой a, основание — b. Стало быть, раз у треугольника есть два «бедра» одной величины, то и углы на «фундаменте» тоже будут одинаковыми. Их назовем «альфа».
Для того чтобы ответить, как найти сторону равнобедренного треугольника, необходимо ввести еще одну величину — угол, образованный между равными «бедрами».Так как он располагается напротив b, то назвать его лучше всего «бета». Здесь при поиске неизвестных сторон можно пользоваться несколькими формулами. Давайте же посмотрим, какими именно.
Первые две — это те, по которым можно вычислить длину стороны основания равнобедренного треугольника. Основана она на знаниях ученика о синусах и косинусах.Итак, выглядят наши вычисления следующим образом: b=2*a*sin(«бета»/2)=a*(2-2*cos»бета»)^(1/2) или же b=2*a*cos»альфа». Легко все и просто. Особенно, если «набить руку» и попрактиковаться.
Какую именно запись нужно использовать? Все зависит от поставленной задачи и условий. Конечно же, можно произвести проверку вычислений по всем формулам, если у вас есть абсолютно все данные. Теперь можем двигаться дальше.
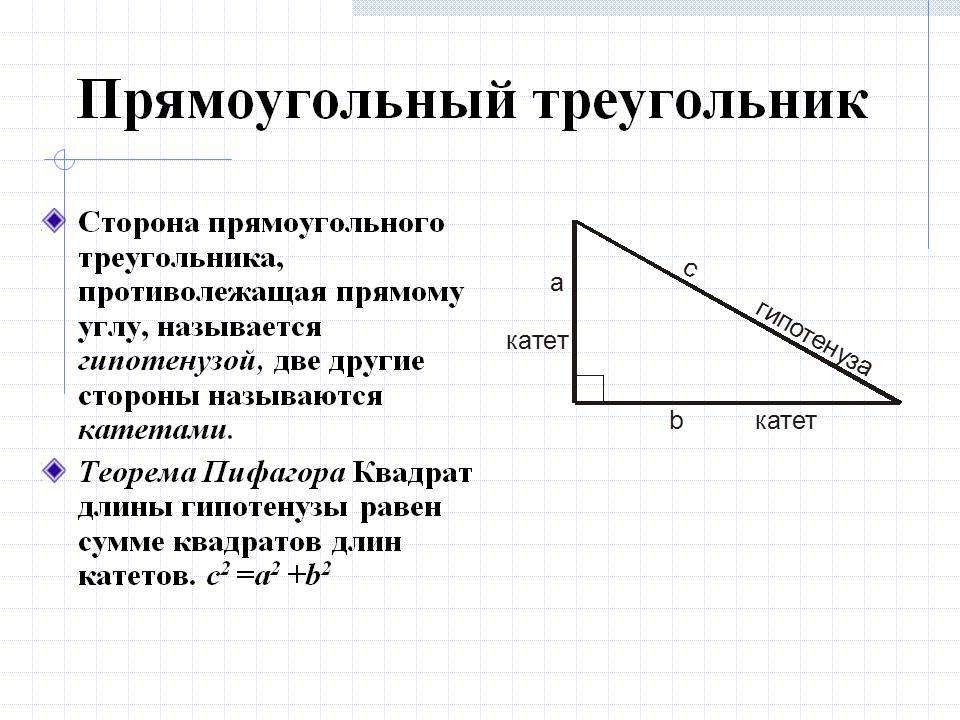
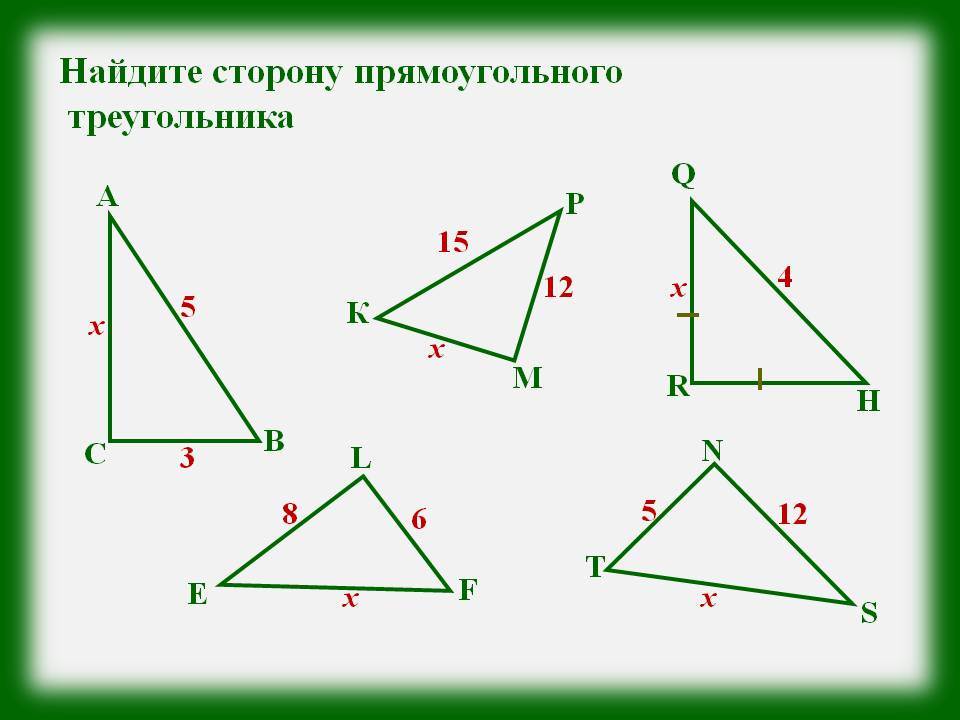
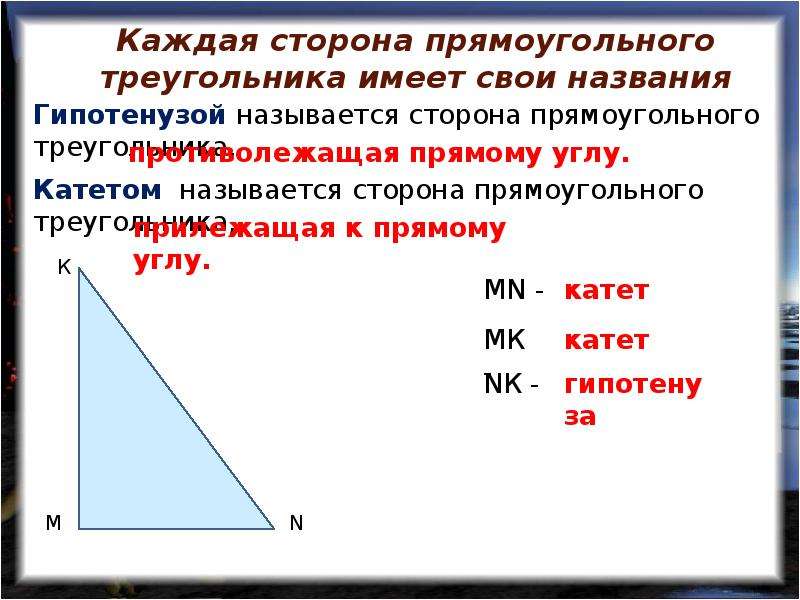
Прямоугольный треугольник
Наверное, каждый школьник, который только начал изучение геометрии, знает, что такое прямоугольный треугольник. С первого взгляда в данной фигуре нет ничего особенного, сложного и непонятного. Но вот когда «теряются» данные о той или иной стороне сего геометрического объекта, начинаются проблемы.
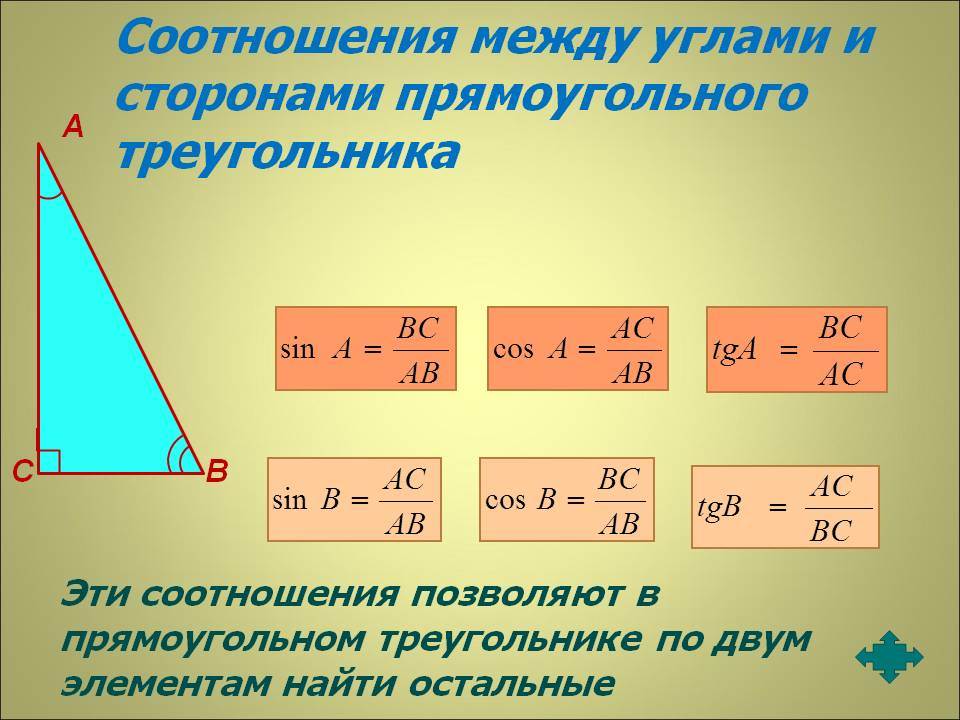
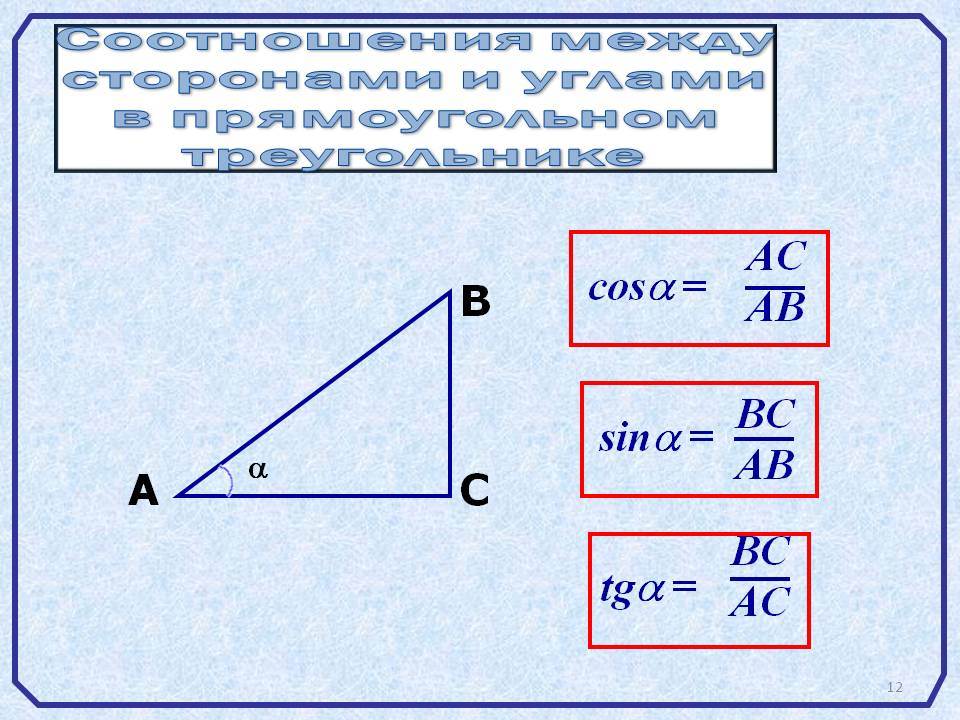
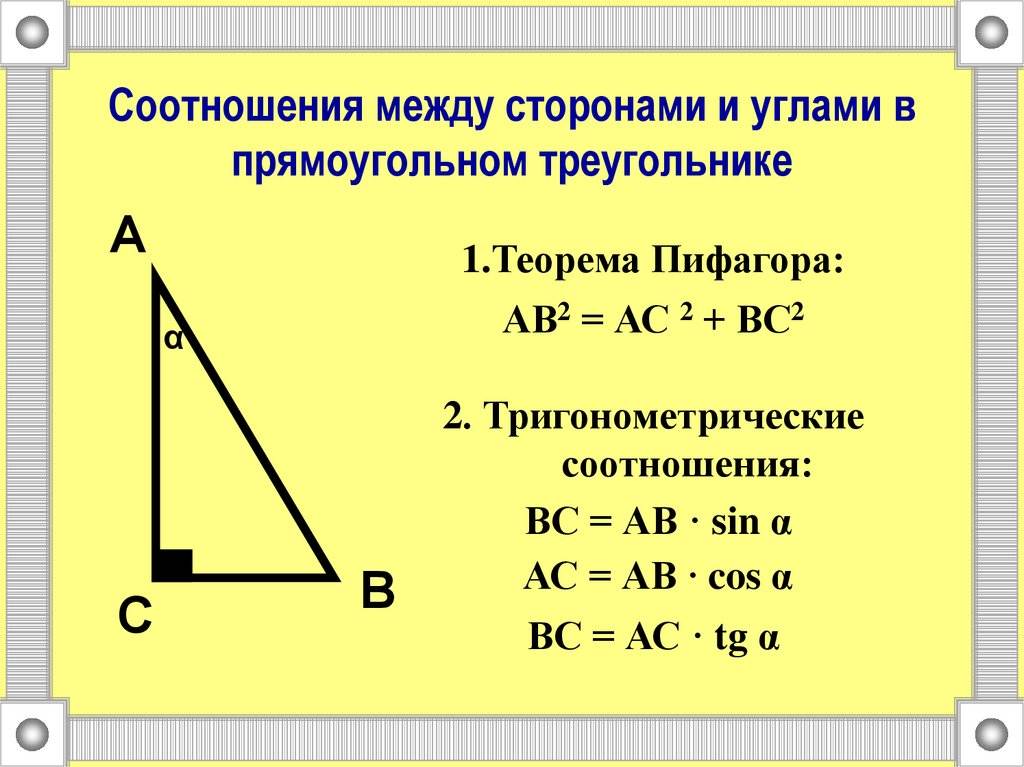
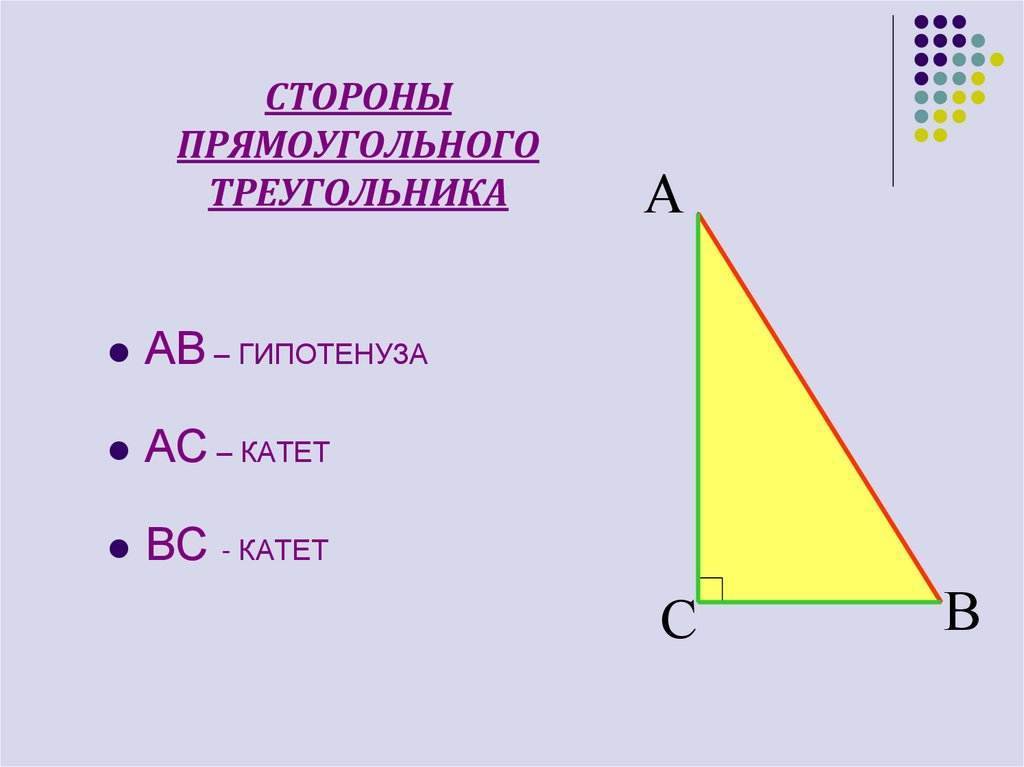
Дело все в том, что вопрос: «Как найти сторону прямоугольного треугольника?» — затрагивает не только понятия синуса и косинуса, а еще и тангенсов углов. Таким образом, вычисления становятся намного сложнее и больше. Итак, сначала обозначим два катета нарисованного прямоугольного треугольника через a и b.
Углы, лежащие напротив этих сторон, как и принято было прежде, назовем «альфа» и «бета» соответственно. Нашей гипотенузой будет служить сторона c. Угол, лежащий против него, нам не понадобится — он будет прямым. Вариантов вычислений тут несколько. Первый называется классическим. Для катета a формулы выглядит как: a=c*cos»бета»=c*sin»альфа»=b*tg»альфа».
Значит, будем иметь следующее: a=(c*c-b*b)^(1/2), b=(c*c-a*a)^(1/2), c=(b*b+a*a)^(1/2). Вот простой и незамысловатый ответ на вопрос, как найти сторону треугольника. Не пугайтесь огромных вычислений.
Итоги
Итак, сегодня мы разобрались, как найти сторону треугольника, и выучили много новых формул. Для того чтобы лучше их запомнить, запишите их на какую-нибудь бумажку, по которой потом будет проще учить все наизусть. Не стоит пугаться «страшных» цифр и больших вычислений. Все проще, чем кажется.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
Так как △AMN ~ △ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.
Так как △AMN ~ △ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
Теорема доказана.
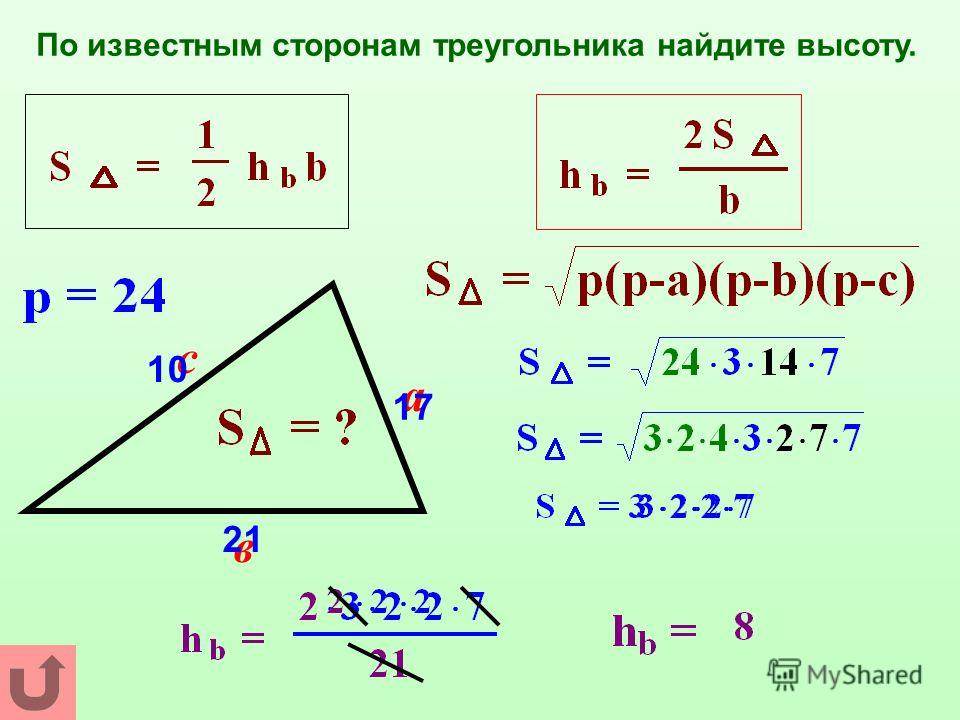
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Решение:
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
S = ½ × AC × BC
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
MN = ½ × AC
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
NP = ½ × BC
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Свойства сторон треугольника
Треугольник имеет важные свойства и характеристики.
Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.
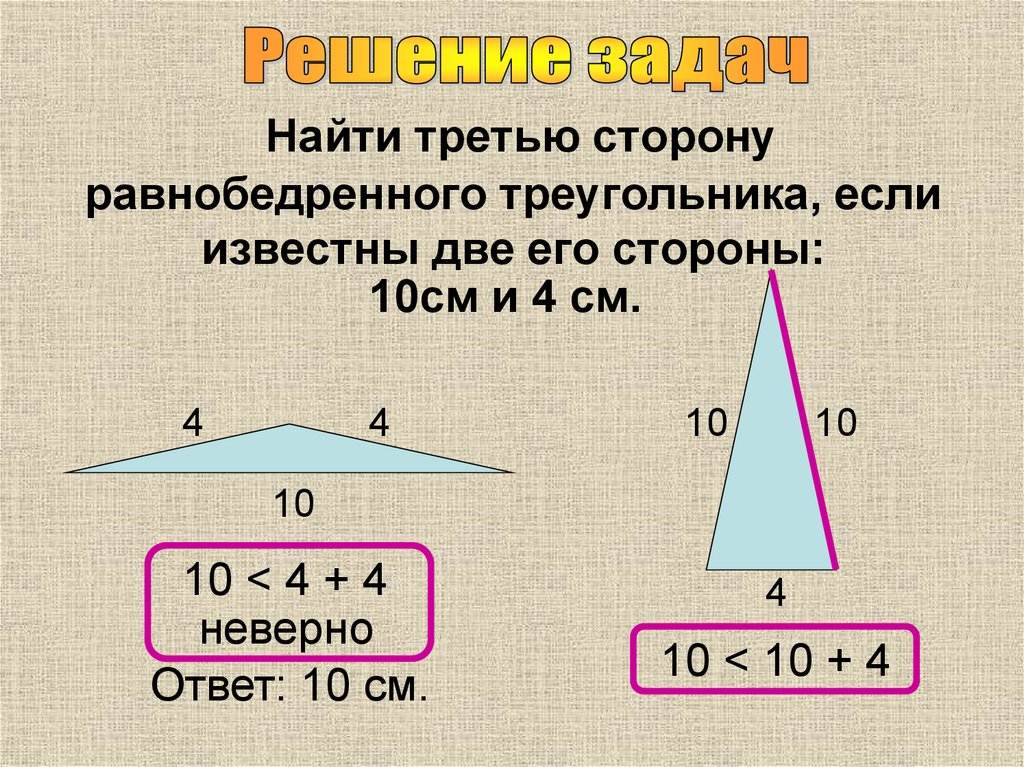
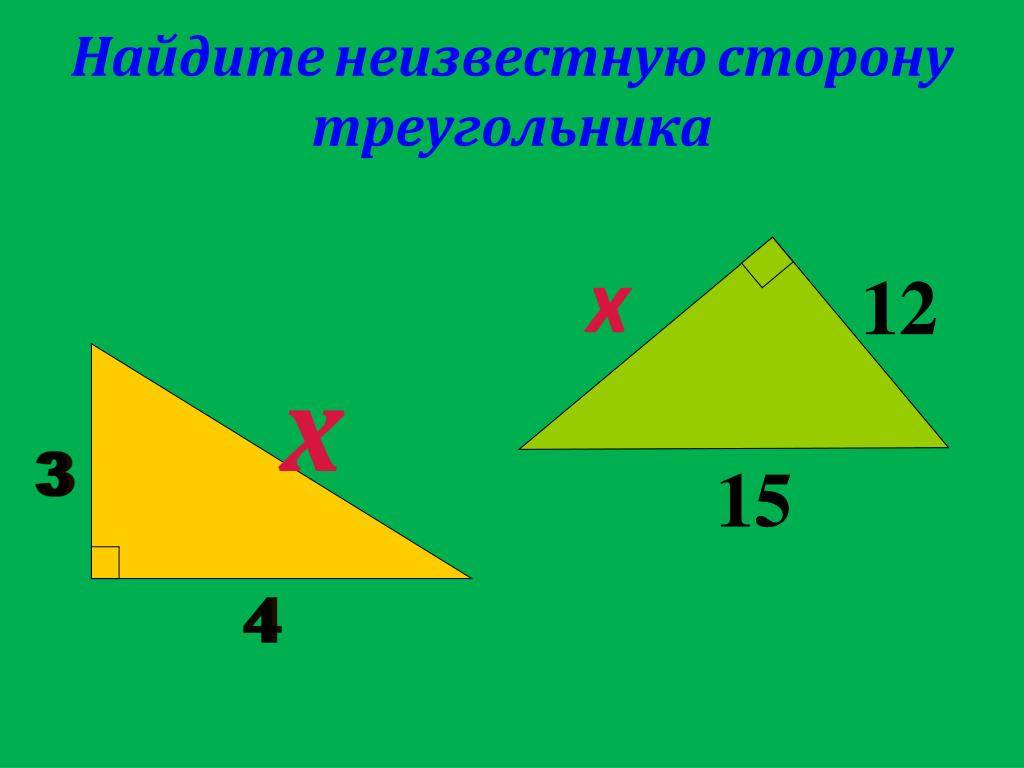
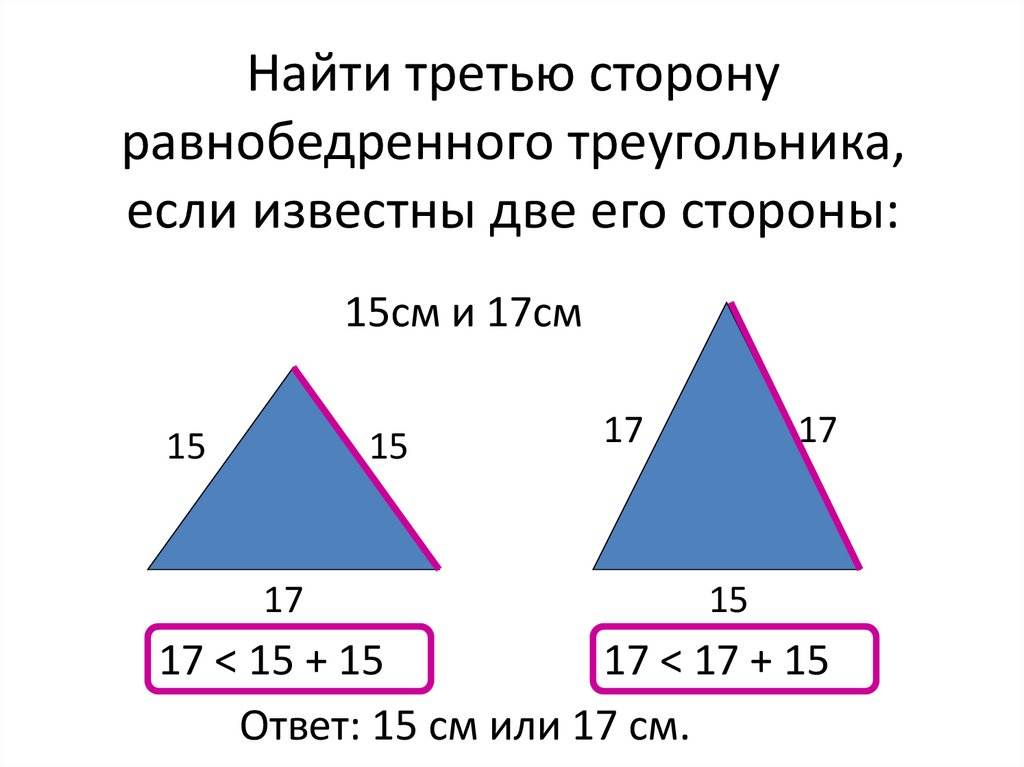
Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?
Решение: согласно свойству сторон треугольника, получим:
, или .
Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.
Правило существования треугольника
Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.
Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?
Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10<15, то есть треугольник не получится.
А вот такие длины сторон 5 см, 7 см и 6 см вполне могут образовать треугольник: складываем 5+6=11 и 11>7 — треугольник с такими длинами сторон существует.
Важные теоремы
Знание теорем для рассматриваемой фигуры позволяет понять, как найти сторону, зная 2 стороны треугольника. Прежде всего применяются две базовые теоремы:
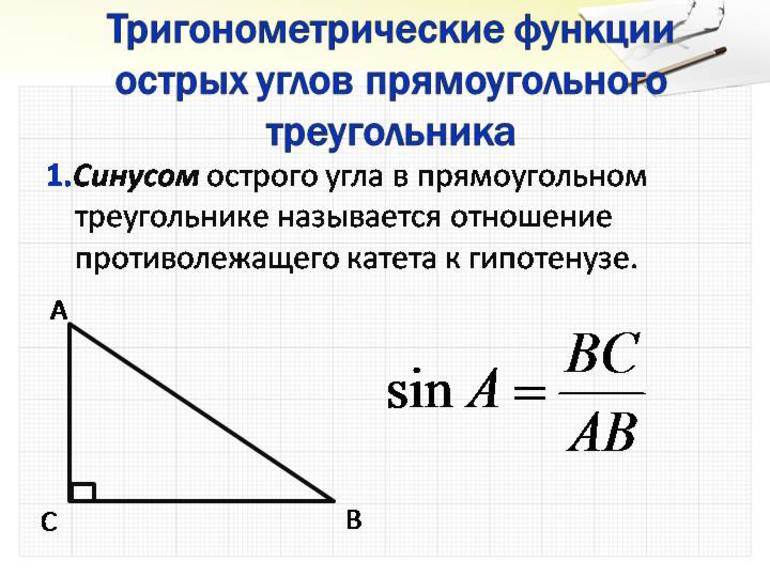
- Синусов. Как известно, синус — это тригонометрическая функция, которая вводится в прямоугольном треугольнике и определяет отношение противолежащего углу катета к гипотенузе. Теорема синусов для фигуры произвольного типа устанавливает следующее математическое взаимоотношение между отрезками и углами: a/sinA = b/sinB = c/sinC. Это означает, что вычислить длину любой стороны можно, если известен еще какой-нибудь отрезок и два угла.
- Косинусов. Как и синус, косинус тоже является тригонометрической функцией, которая определяет отношение катета прилежащего к гипотенузе прямоугольной фигуры. Теорему косинусов удобно записать в виде следующего математического выражения: c 2 = a 2 + b 2 — 2*a*b*cosC. С помощью этого равенства можно найти 3 сторону треугольника по 2 сторонам известным и углу между ними.
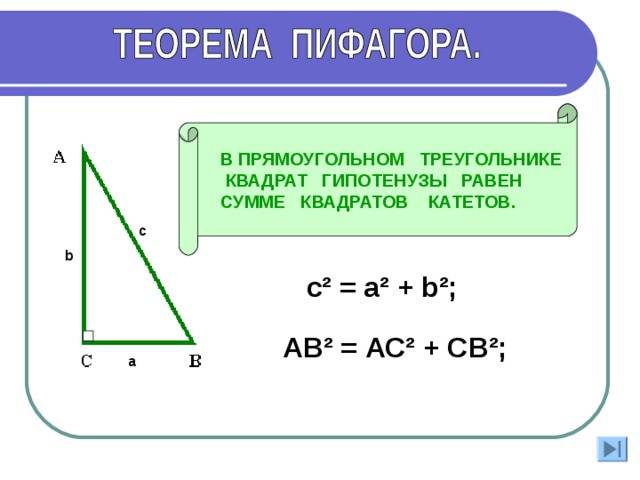
Первое выражение базируется на знаменитой теореме Пифагора, которая устанавливает связь между длинами двух катетов (меньшие стороны) и гипотенузы (большая сторона) в треугольнике с прямым углом. Если гипотенузу обозначить буквой c, тогда будет выполняться следующее равенство:
c 2 = a 2 + b 2 .
Если известные любые две стороны, то для определения третьей достаточно взять под квадратный корень соответствующую сумму или разницу квадратов.
Вторая из дополнительных теорем носит название философа Аполлония Пергского. Соответствующее ей математическое выражение выглядит так:
a 2 + b 2 = ½*c 2 + 2*Mc 2 .
Здесь Mc — это медиана, проведенная к стороне c из вершины C. Это равенство также называют в математике теоремой медианы.
Примеры решения задач

После того как изучены и рассмотрены основные понятия, свойства и теоремы для различного рода треугольников, можно переходить к решению геометрических задач. Поскольку для этого требуется в большинстве случаев знать значения тригонометрических функций, рекомендуется воспользоваться либо соответствующими таблицами, либо инженерным калькулятором.
Задачи школьного курса с треугольниками, как правило, не являются сложными. Они решаются благодаря однократному применению какого-либо свойства или теоремы.
Квадрат и его диагональ
Пусть дан квадрат, сторона которого составляет 11 см. Необходимо определить половину длины его диагонали.
Эту геометрическую задачу проще всего решить, если увидеть, что две смежные стороны исходной фигуры и ее диагональ образуют прямоугольный треугольник, который к тому же является равнобедренным. Каждая из равных сторон в нем имеет длину 11 см и является катетом. Диагональ c — это гипотенуза. Применяя пифагорову теорему, можно получить следующее равенство:
c = (11 2 + 11 2 )^0,5 ≈ 15,556 см.
Поскольку половина диагонали в два раза меньше гипотенузы, то искомым ответом на задачу будет число c/2 ≈ 7,778 см.
Две высоты и угол
Дан треугольник ABC. Известно, что при вершине C угол составляет 37 °. Из вершин A и B проведены высоты к сторонам этого треугольника, их длины составляют h1 = 10 см и h2 = 8 см, соответственно. Необходимо узнать длину стороны фигуры, которая лежит против угла C.
Из условия задачи можно найти длины сторон AC и BC. Для этого следует увидеть, что каждая из высот с двумя другими сторонами треугольника образует прямоугольную фигуру. Воспользовавшись тригонометрическими равенствами, можно получить следующие результаты:
- AC = h1/sinC = 10/sin (37 °) ≈ 16,616 см;
- BC = h2/sinC = 8/sin (37 °) ≈ 13,293 см.

Против угла C лежит сторона AB, которую следует найти. Получается, что известны две стороны треугольника (AC и BC) и угол между ними. Остается применить теорему косинусов, чтобы получить ответ:
AB = (AC 2 + BC 2 — 2*AC*BC*cosC)^0,5 = (16,616 2 + 13,293 2 — 2* 16,616 * 13,293 *cos (37 °))^0,5 ≈ 10 см.
Полученный результат свидетельствует о том, что высота h1 совпадает со стороной AB с рассчитанной точностью, то есть исходный треугольник являлся прямоугольным.
Таким образом, для нахождения стороны треугольника, если известны две другие его стороны или иные отрезки, следует воспользоваться теоремами. Основными из них являются теорема косинусов и синусов, а также Пифагора и Аполлония.