Свойства прямоугольного треугольника
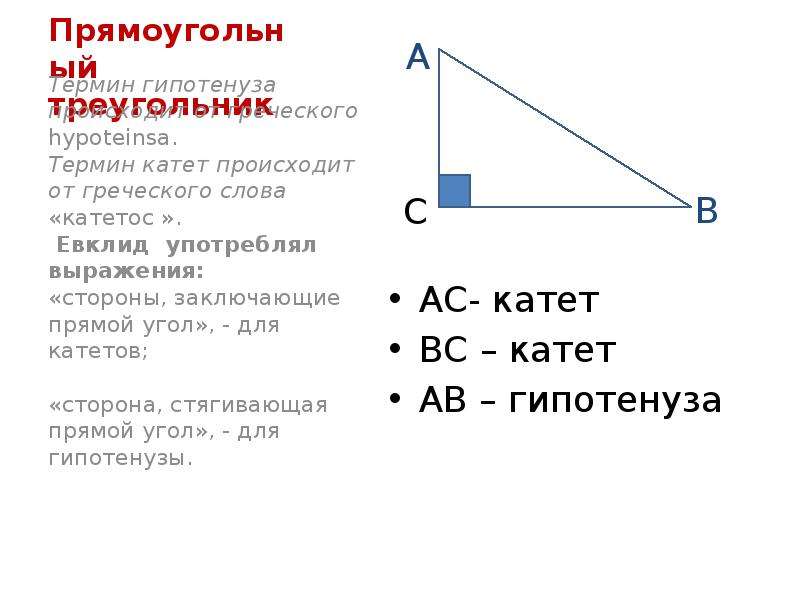
Прямоугольный треугольник — это симметричный многоугольник, сумма двух углов которого равняется 90 градусов. Так как общая сумма всех трёх углов составляет 180 градусов, то соответственно третий угол равен 90 градусам. Стороны, образующие его, называют катетами, а оставшийся отрезок гипотенузой.
К основным свойствам фигуры относят следующее:

- гипотенуза многоугольника всегда больше любого из его катетов;
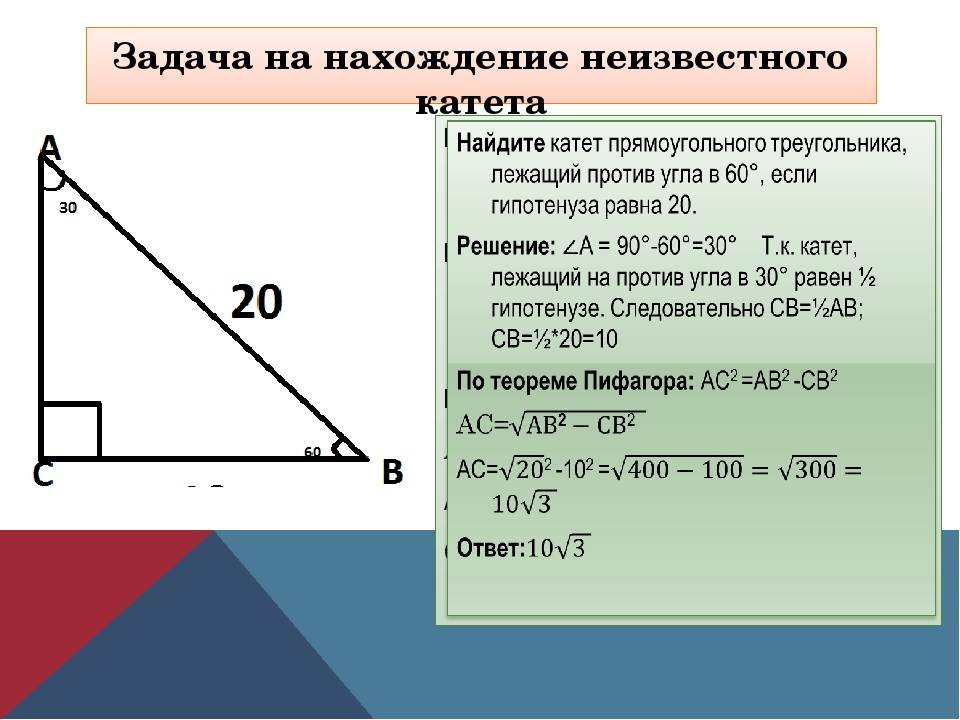
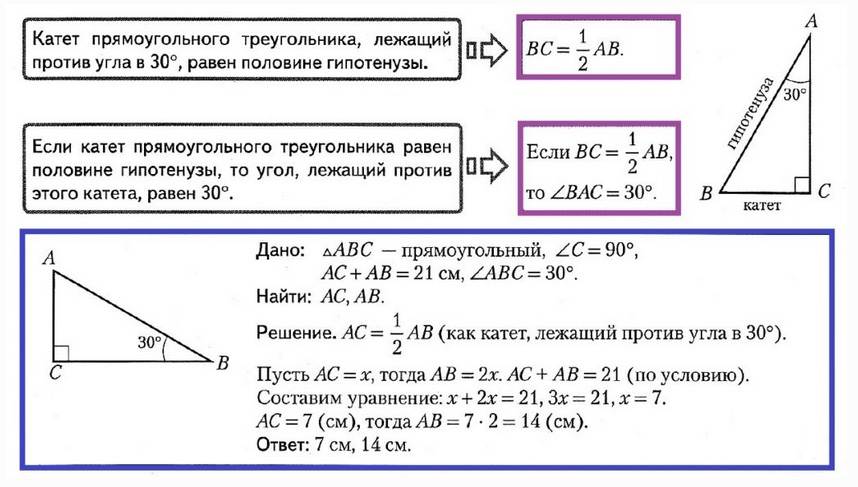
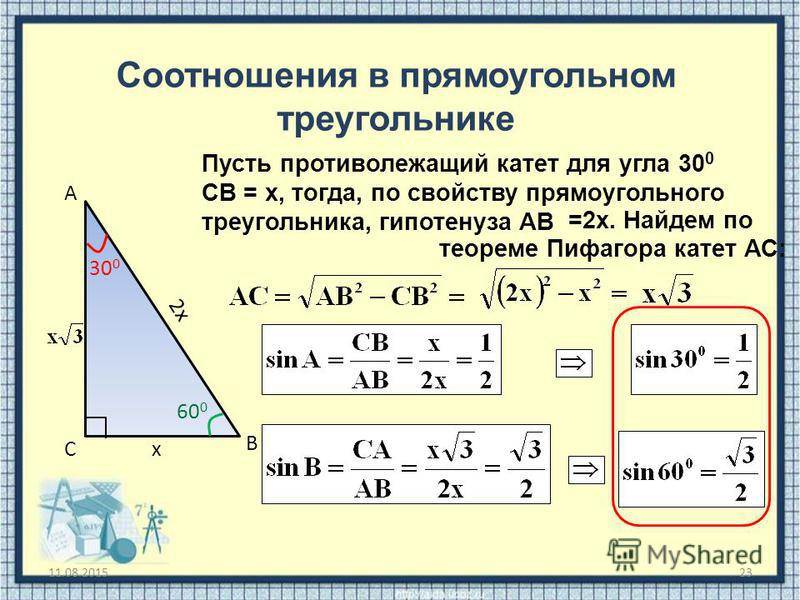
- сторона, располагающаяся напротив угла в 30 градусов, составляет половину гипотенузы;
- два катета являются высотами треугольника;
- середина окружности, описанная вокруг фигуры, совпадает с гипотенузой, при этом медиана, опущенная из прямого угла на гипотенузу, одинаковая с радиусом круга;
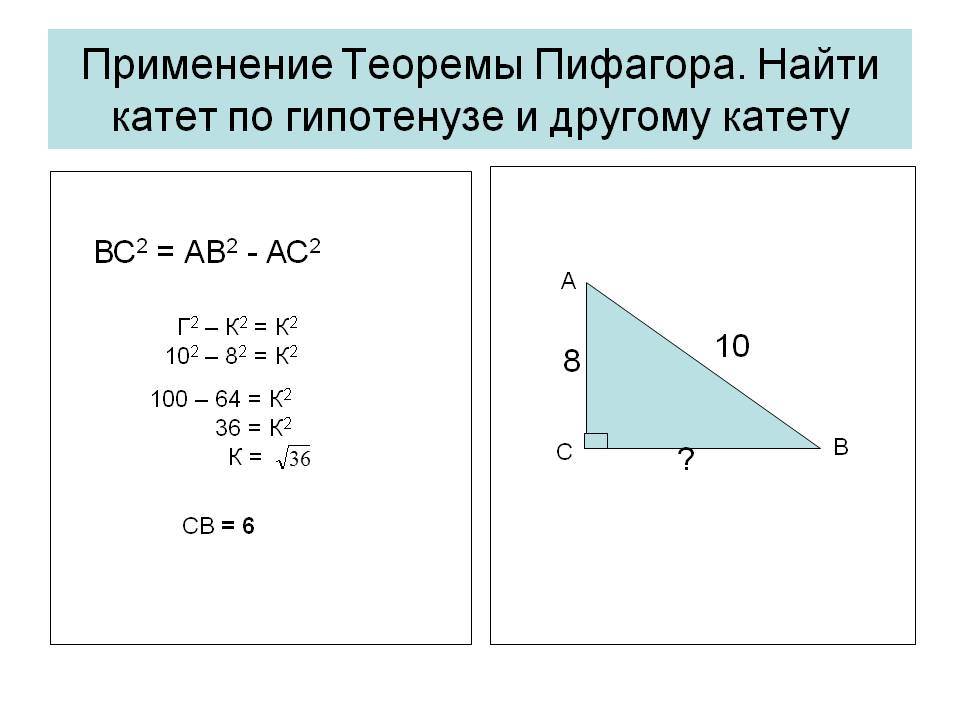
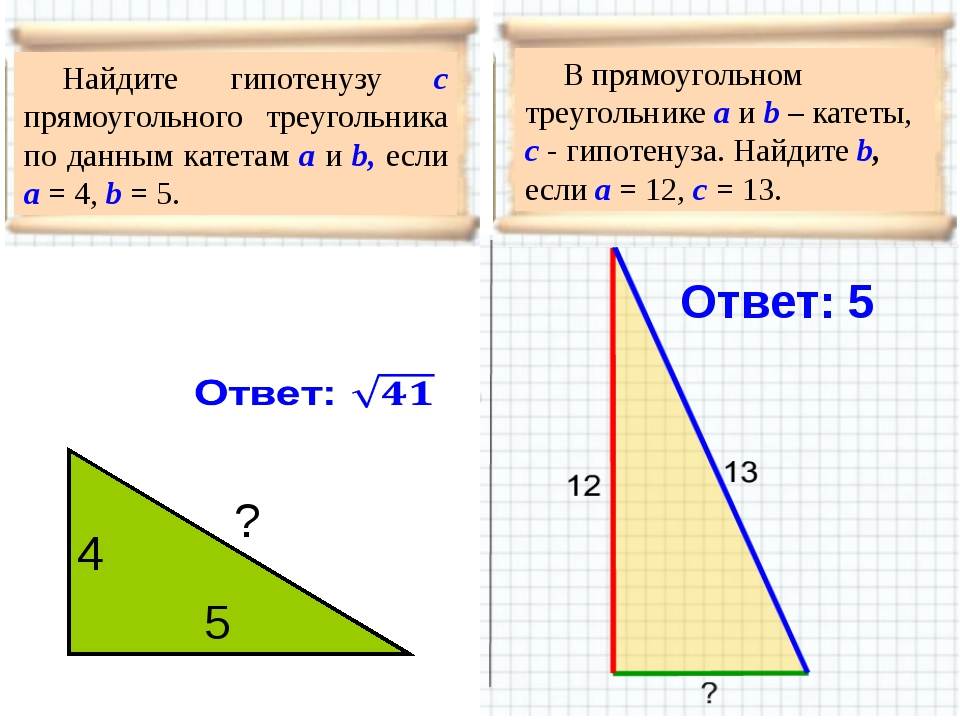
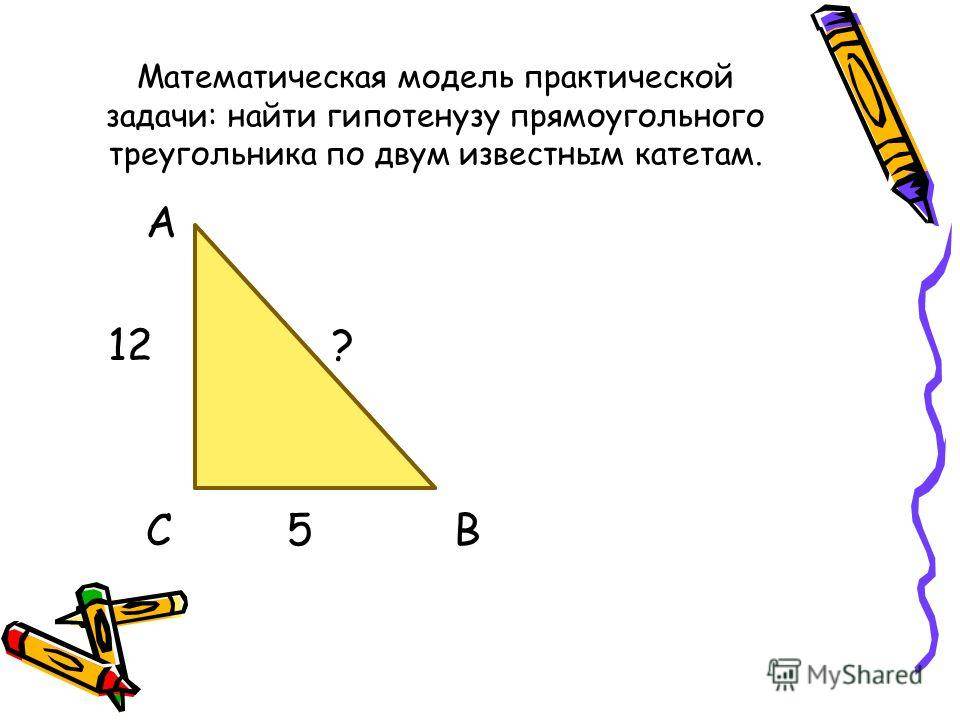
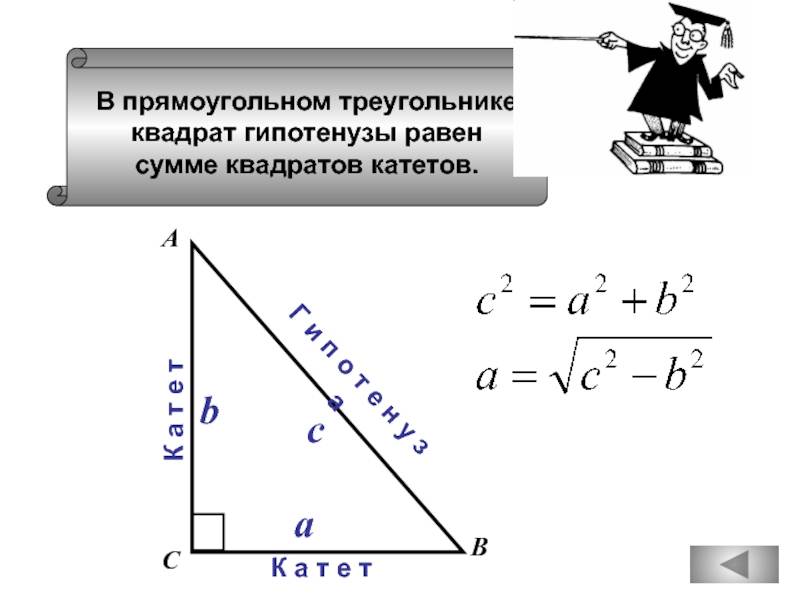
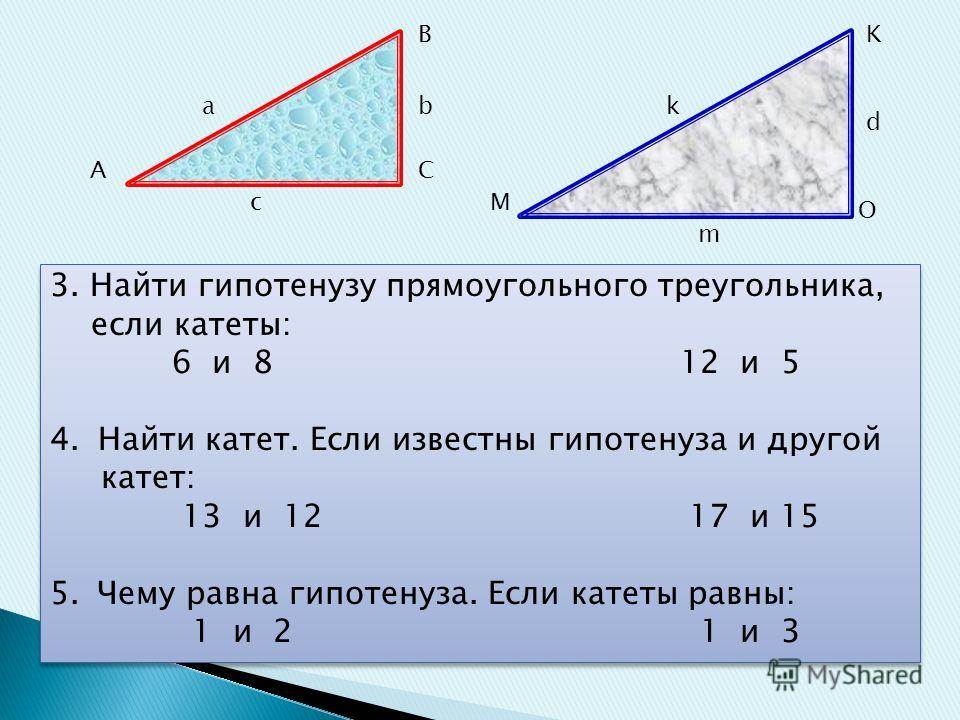
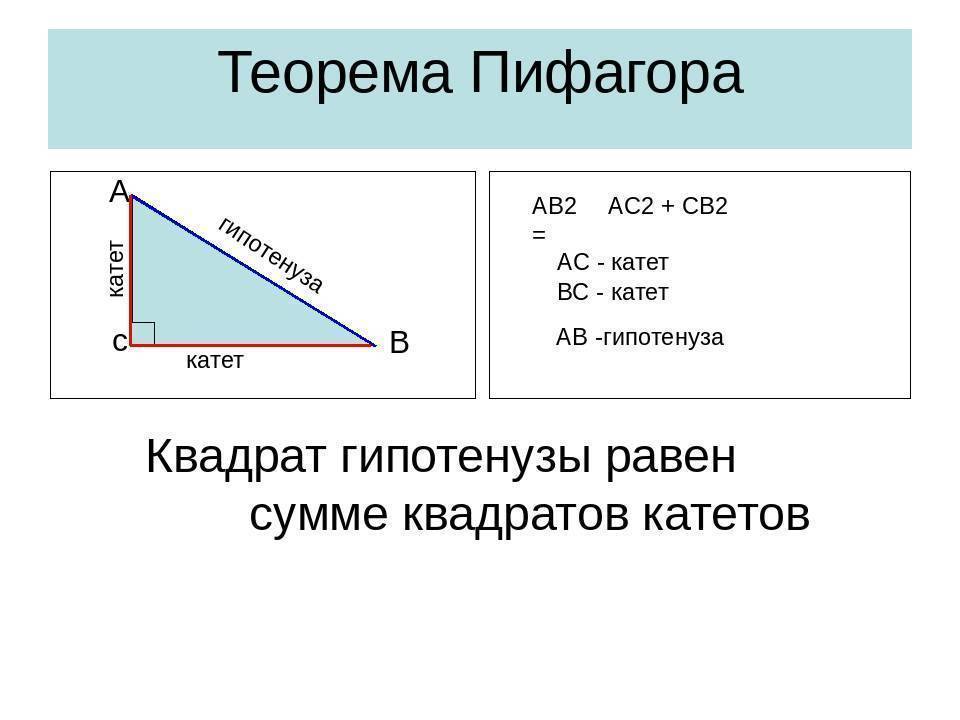
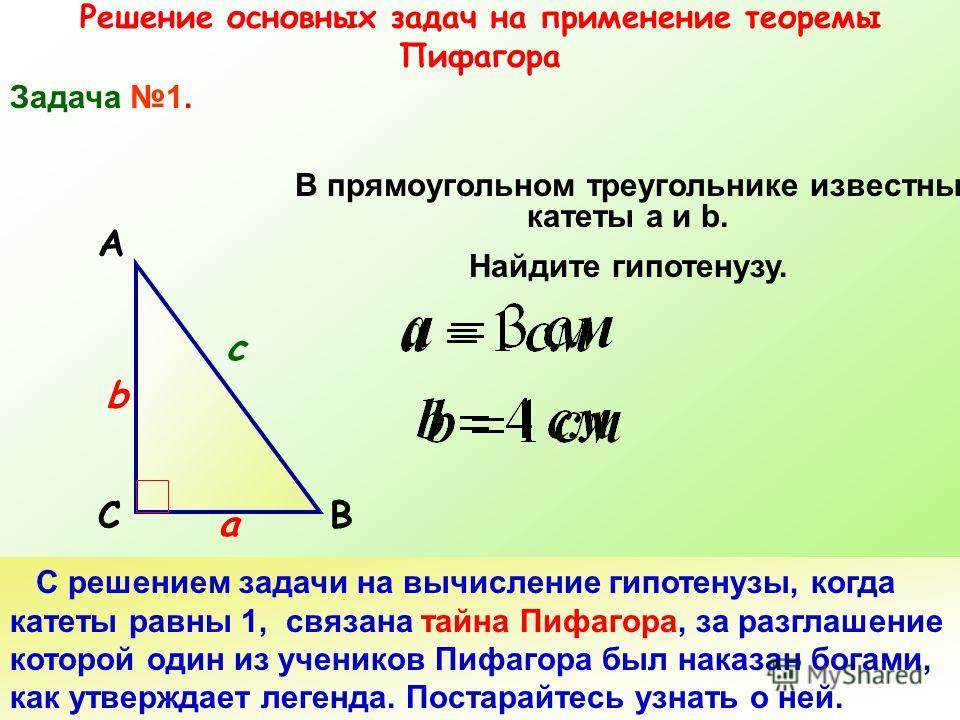
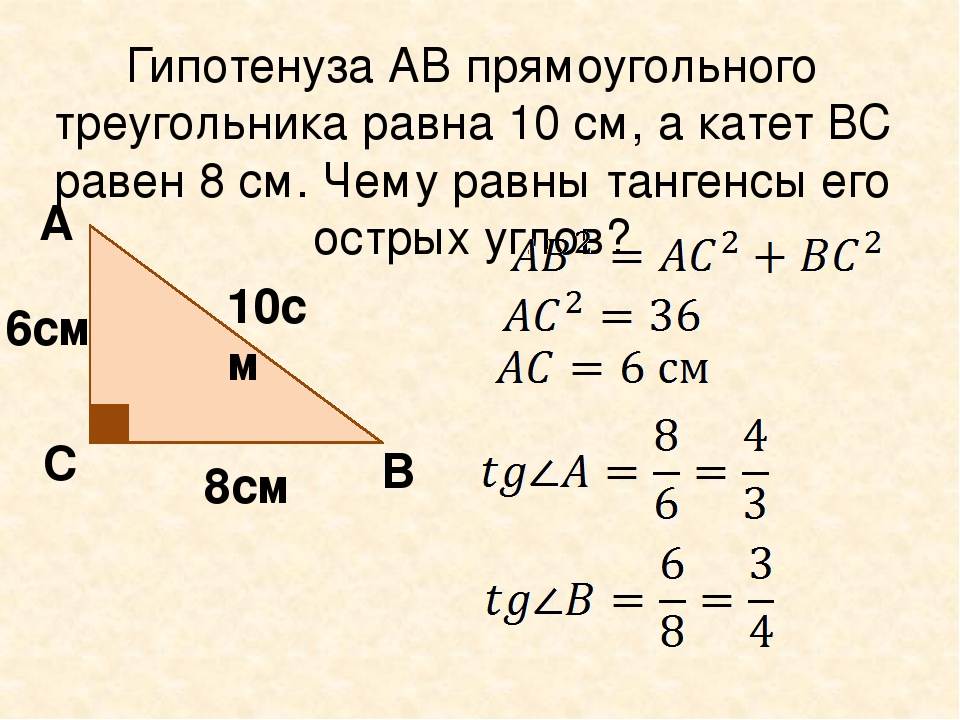
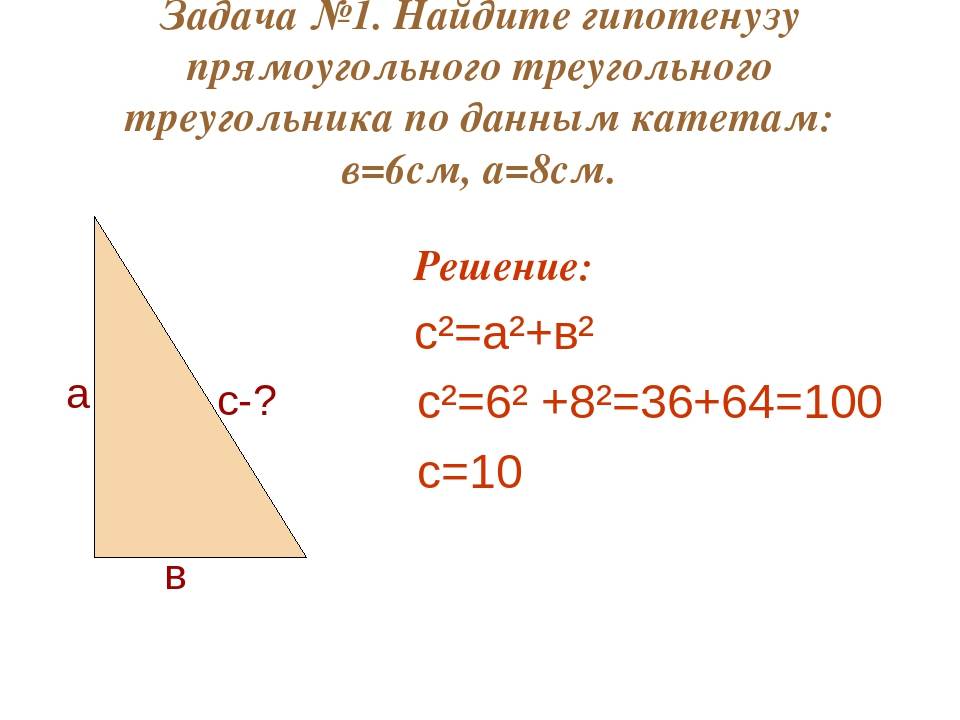
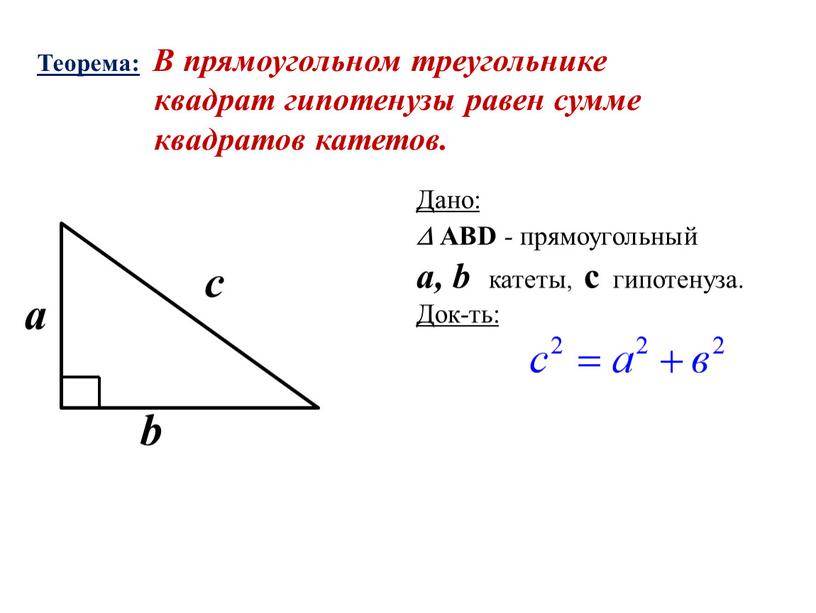
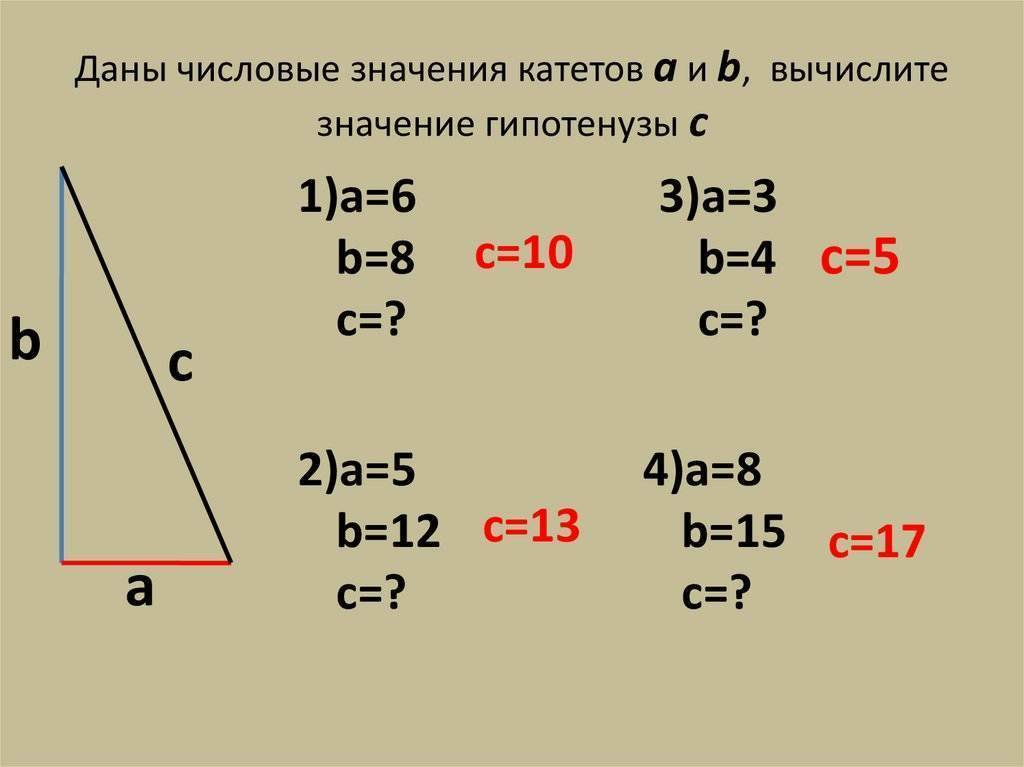
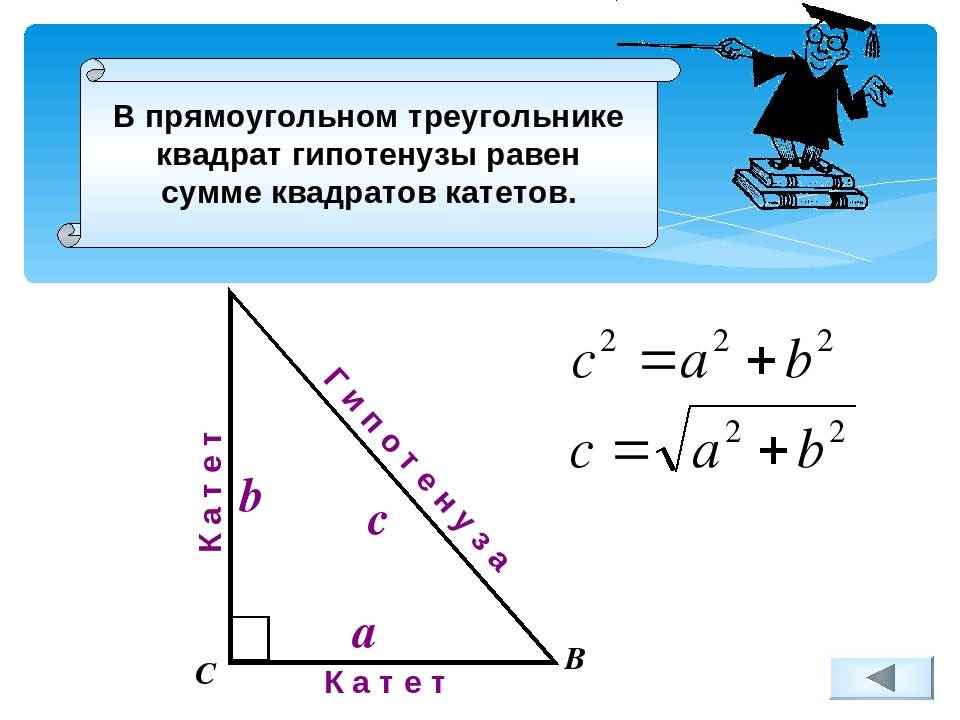
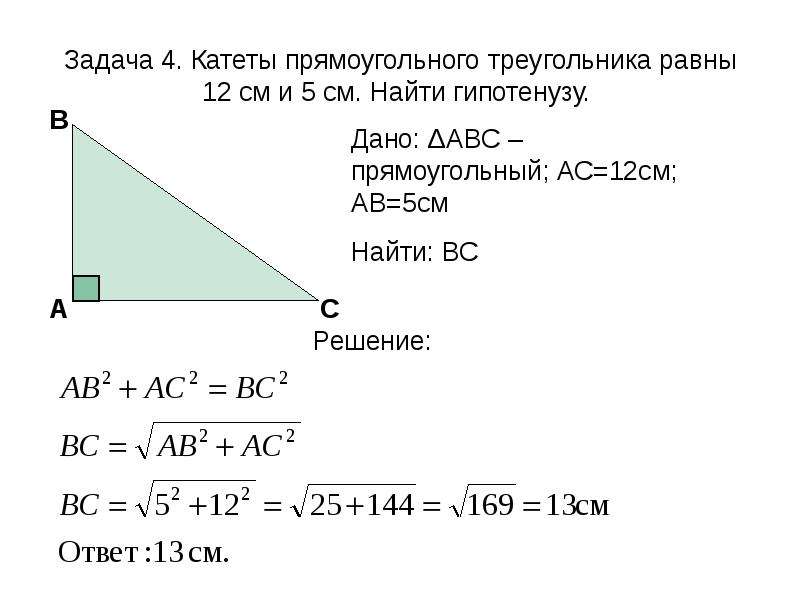
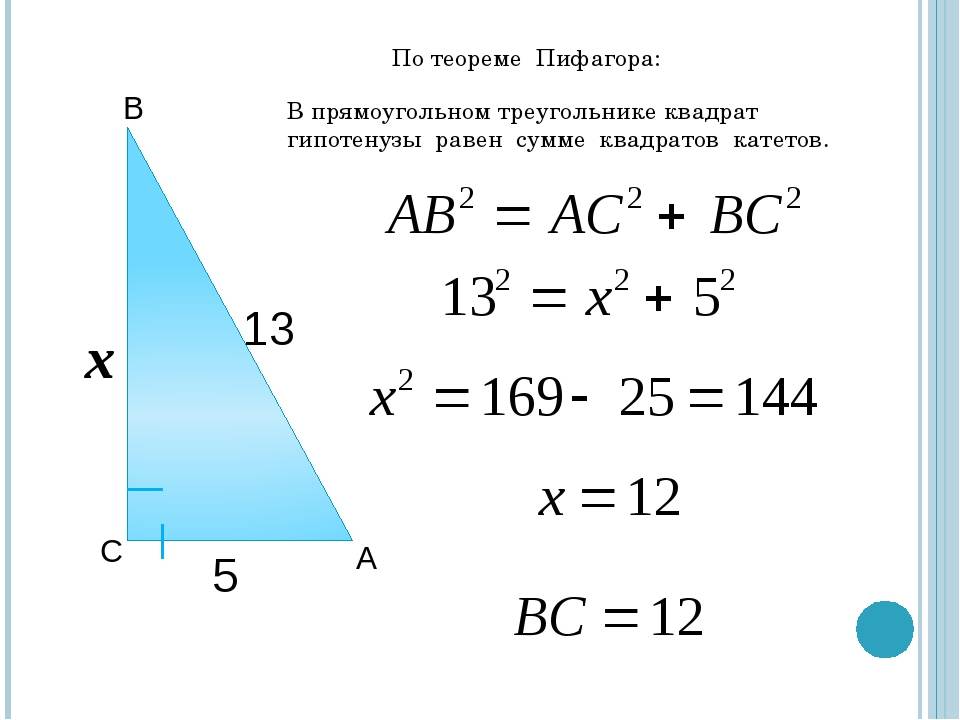
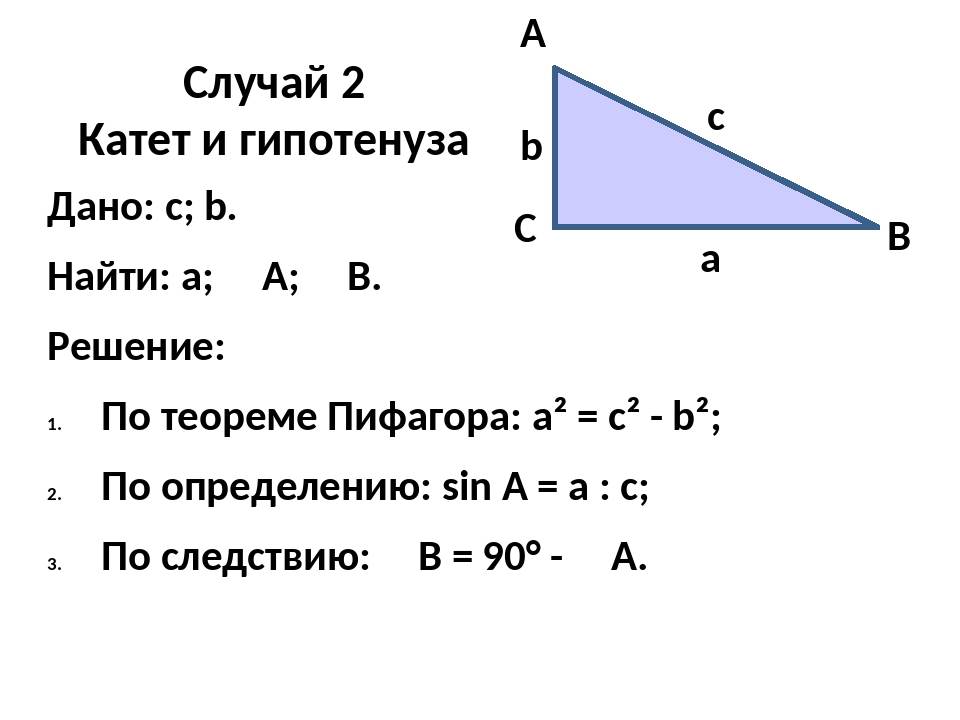
- численное значение гипотенузы, возведённое в квадрат, равно сумме квадратов катетов (теорема Пифагора).
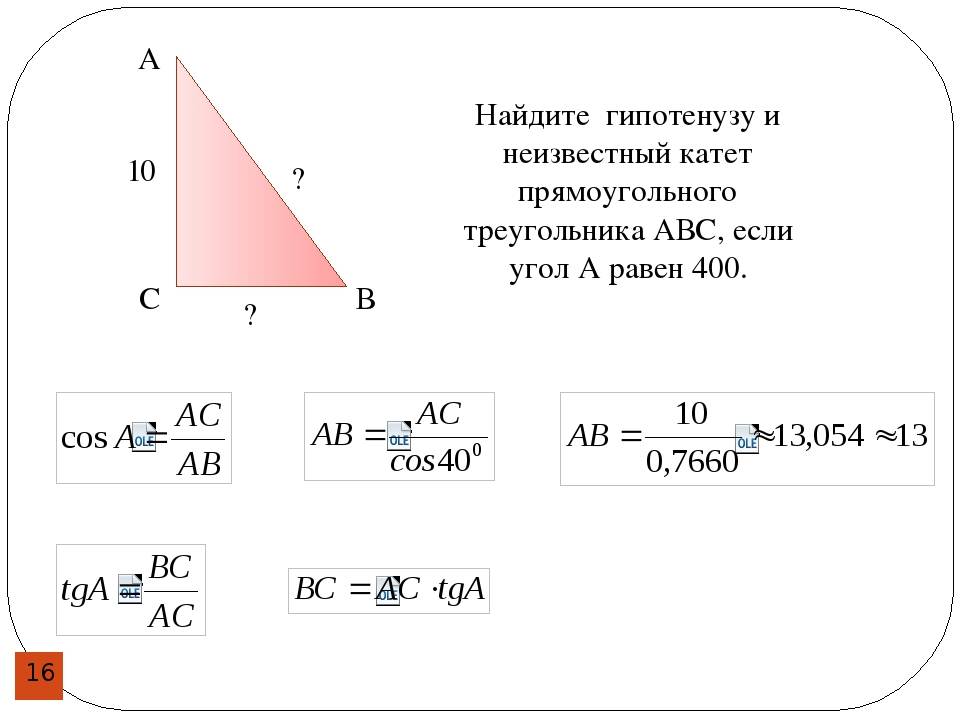
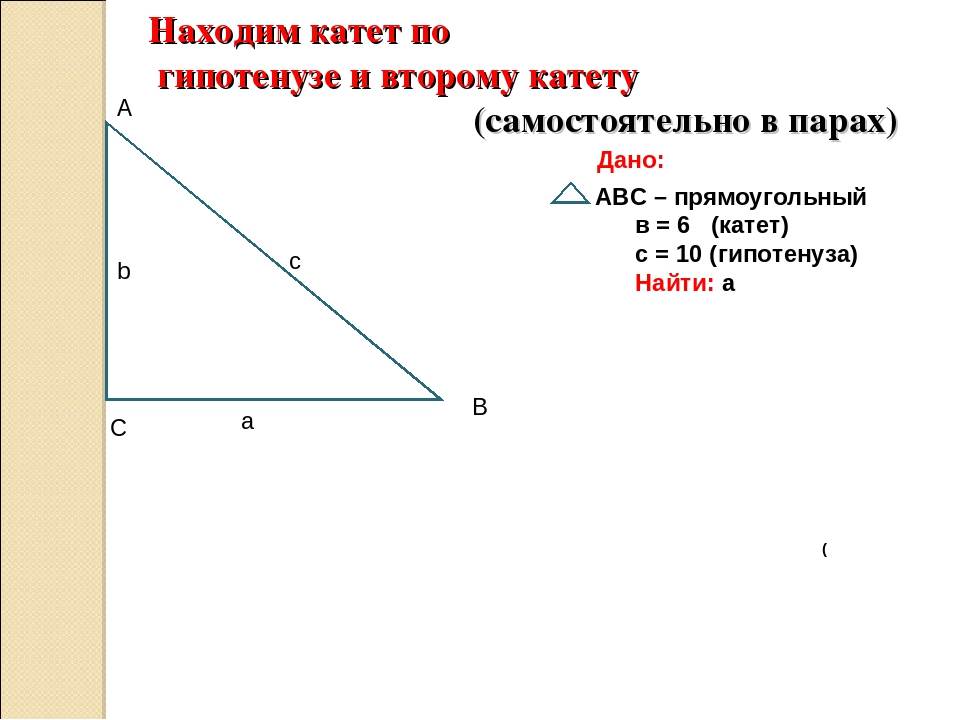
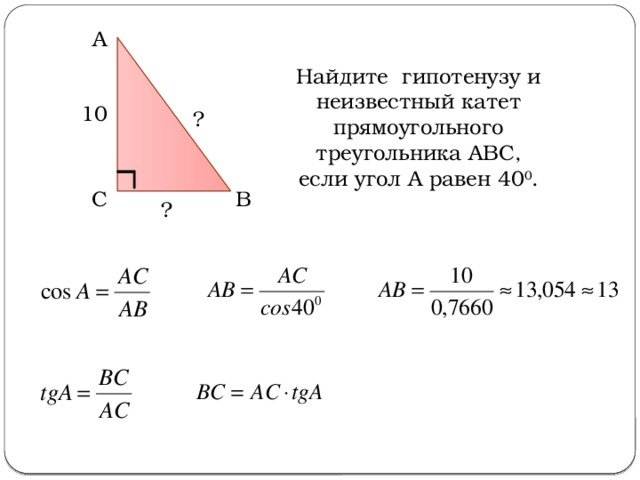
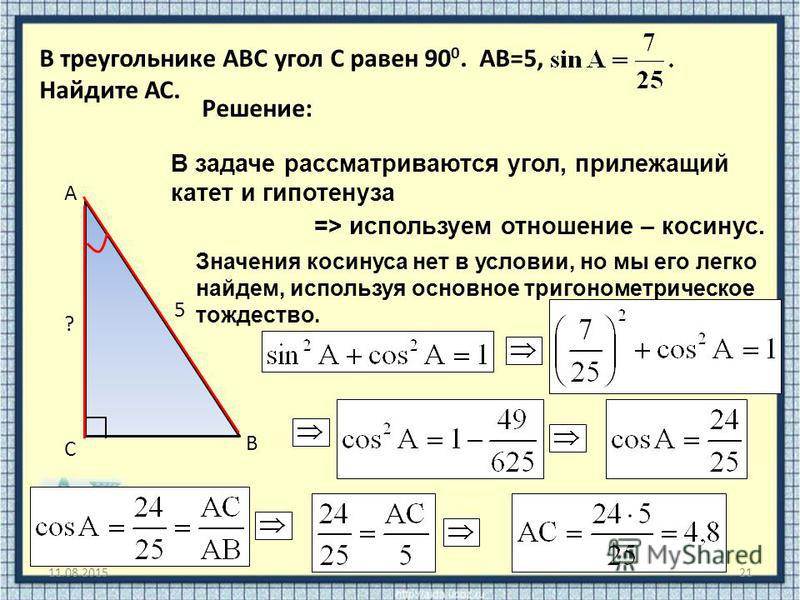
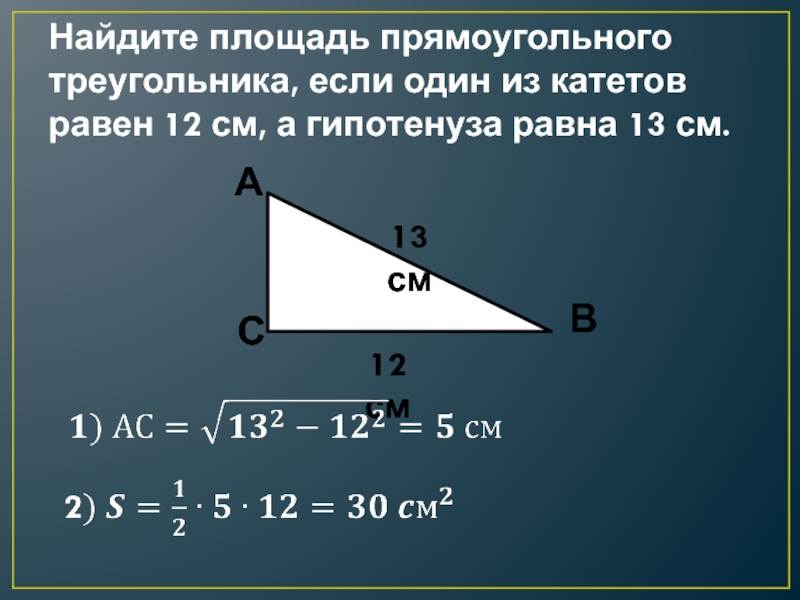
Так, если известна гипотенуза, то найти катеты, зная угол, не составит труда. Определив же длину катетов, вычислить оставшуюся сторону можно по теореме Пифагора. Периметр фигуры определяют сложением двух катетов и гипотенузы, а площадь находят перемножением катетов и делением полученного ответа на два.

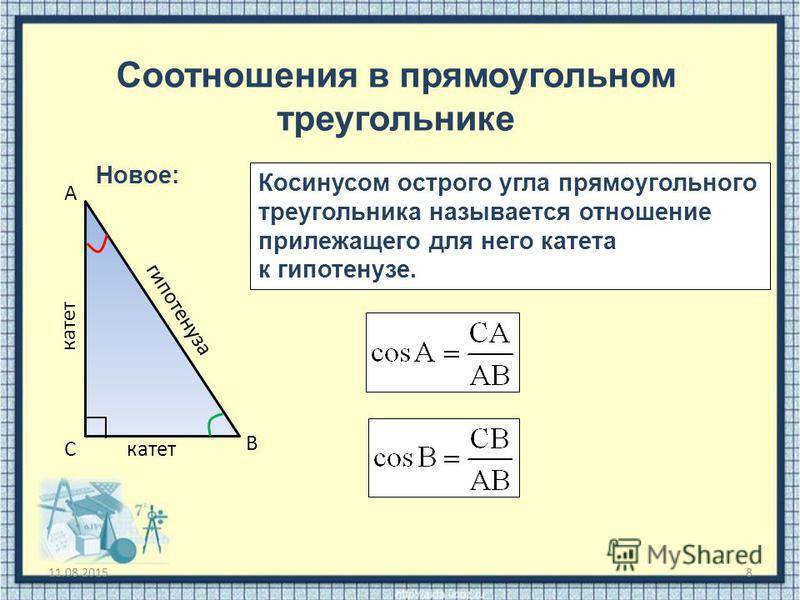
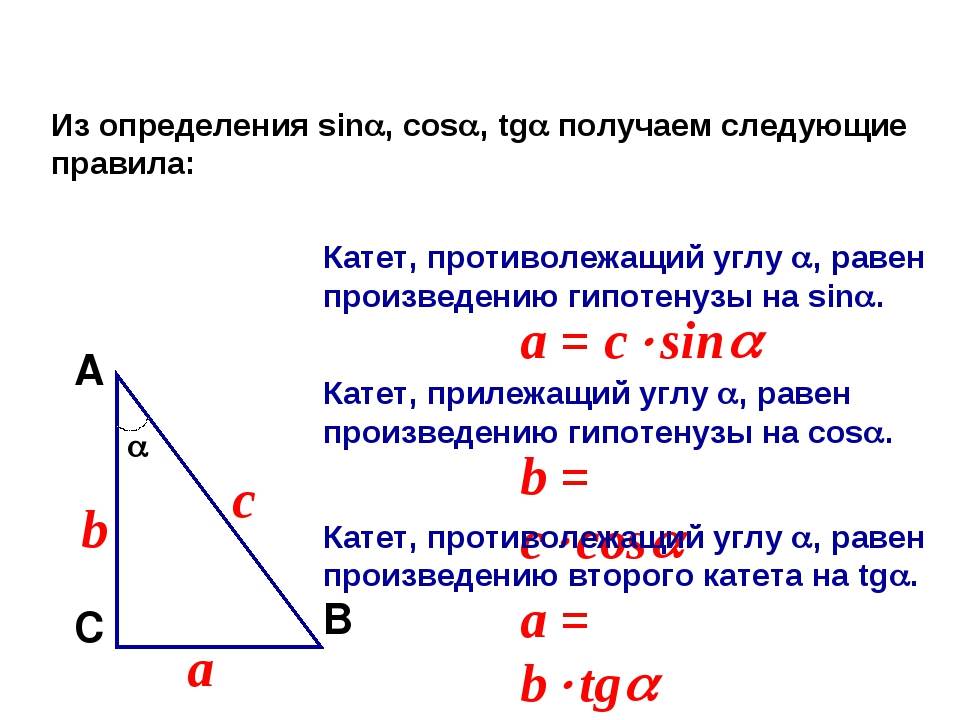
Зная катеты, довольно просто вычислить угол. Нужно всего лишь запомнить, что соотношение сторон между собой равно тангенсу противолежащего угла и котангенсу, находящемуся рядом. При этом, зная любой из углов, найти второй можно простым вычитанием известного значения из девяноста. Высота же у прямоугольника равна косинусу прилежащего угла.
Формула для нахождения биссектрисы и медианы довольно сложная. Для нахождения первой величины используют преобразование радикала из суммы квадратов катетов к двум, а второй – подстановку радикала вместо стороны, лежащей напротив прямого угла.
Пример задачи №2
Условие: вычислить диагональ, проведенную в прямоугольнике с меньшей стороной, равной 41. Если известно, что она делит угол на такие, которые соотносятся как 2 к 1.
Решение.
В этой задаче диагональ прямоугольника является наибольшей стороной в треугольнике с углом 90º. Поэтому все сводится к тому, как найти гипотенузу.
В задаче идет речь об углах. Это значит, что нужно будет пользоваться одной из формул, в которых присутствуют тригонометрические функции. А сначала требуется определить величину одного из острых углов.
Пусть меньший из углов, о которых идет речь в условии, будет обозначен α. Тогда прямой угол, который делится диагональю, будет равен 3α. Математическая запись этого выглядит так:
90º = 3 α.
Из этого уравнения просто определить α. Он будет равен 30º. Причем он будет лежать напротив меньшей стороны прямоугольника. Поэтому потребуется формула, описанная в способе №3.
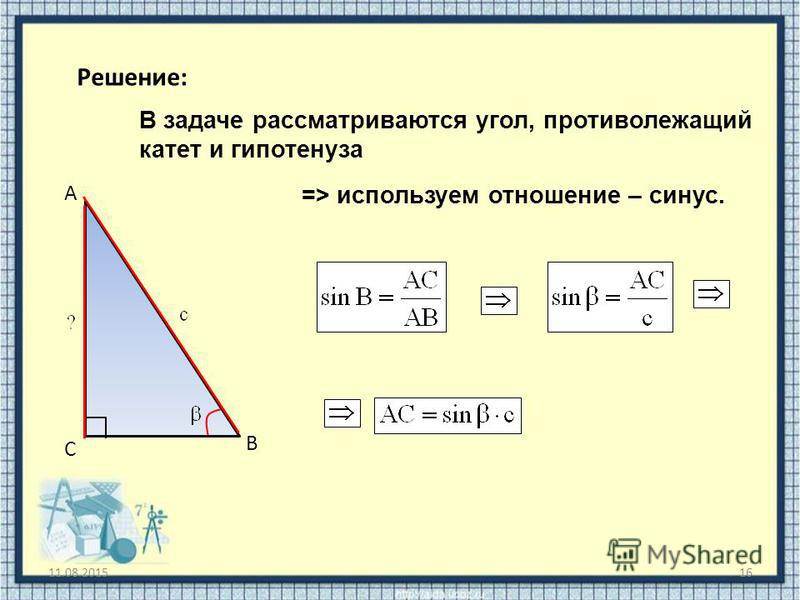
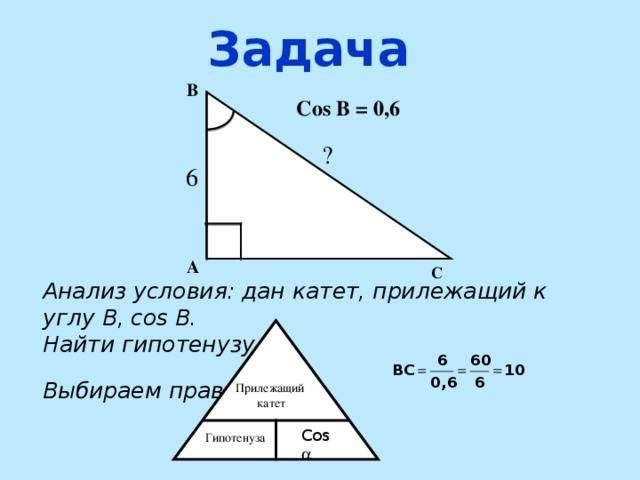
Гипотенуза равна отношению катета к синусу противолежащего угла, то есть:
41 / sin 30º = 41 / (0,5) = 82.
Ответ: гипотенуза равна 82.
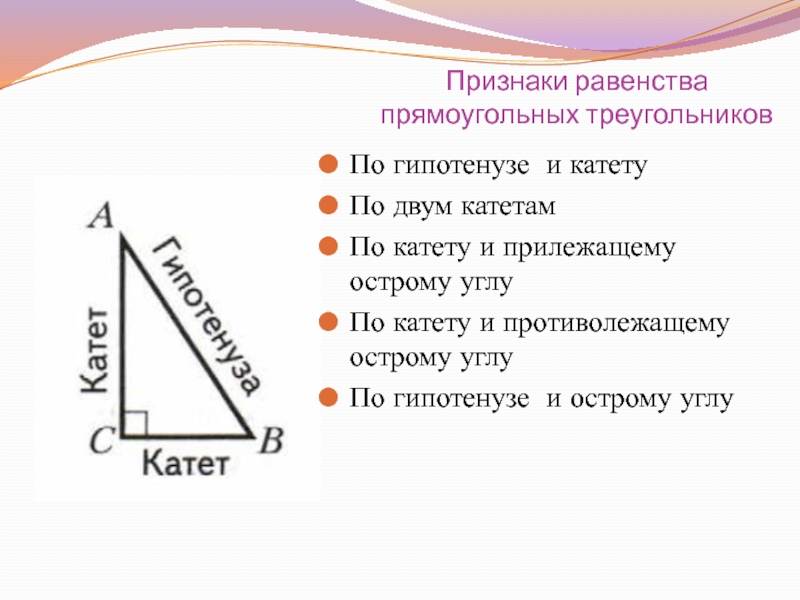
Признаки равенства прямоугольных треугольников
1. Признак равенства прямоугольных треугольников по двум катетам
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то эти треугольники равны.
Действительно. Пусть , (Рис.3). Поскольку , то по первому признаку равенства треугольников следует, что треугольники и равны.
2. Признак равенства прямоугольных треугольников по катету и прилежащему к нему острому углу
Если катет и прилежащий к нему острый угол прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Действительно. Так как , , (Рис.4), то из второго признака равенства треугольников следует, что треугольники и равны.
Теорема 1. Если гипотенуза и прилежащий к нему острый угол прямоугольного треугольника соответственно равны гипотенузе и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство. Пусть и (Рис.5). Так как данные треугольники прямоугольные, то имеет место также равенство . Тогда из второго признака равенства треугольников следует, что треугольники и равны.
4. Признак равенства прямоугольных треугольников по гипотенузе и катету
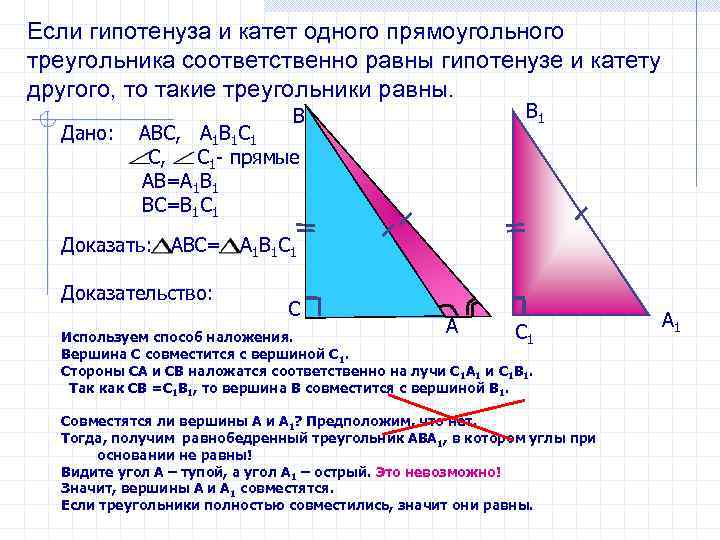
Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Доказательство. Рассмотрим треугольники и , где , и углы C и C1 прямые (Рис.6).
Поскольку , , , то треугольник можно наложить на треугольник так, чтобы вершина C совместилась с верншиной C1 а стороны CA и CB наложились на лучи C1A1 и C1B1, соответственно (Рис.7).
Так как CB=C1B1, то вершина B совместится с вершиной B1. Покажем, теперь, что вершина A совместится с вершиной A1. Предположим, что они не совместятся. Тогда получим равнобедренный треугольник ABA1, поскольку AB=A1B1. Но в этом случае . Но как мы видим из Рис.7 угол , острый а угол тупой (так как он является смежанным углом к острому углу BAC), что невозможно. Следовательно вершина A совместится с вершиной A1.