Как решать уравнения с корнями

Методы решения показательных уравнений

Самые короткие и простые показательные уравнения решаются с помощью элементарной математики. Например:

4х = 64.

Требуется найти, в какую степень нужно возвести 4, чтобы получить 64.

4 × 4 × 4 = 64

43 = 64

Х = 3

Но как решать показательные уравнения вот такого вида: 3√128= 42х? Нужно немного повозиться с преобразованием этого выражения. Например, сделать так, чтобы либо основания, либо степенные показатели стали одинаковы. Для этого мы можем разложить 128 и 4. Вы ведь заметили, что у них есть общий множитель? Правильно, это 2.

3√128= 42х

3√27= (22)2x

27/3 = 24х

Теперь в нашем уравнении появились одинаковые основания, а значит, мы можем приравнять и степени.

4х = 7/3

х = 7/12

В данном случае мы используем один из алгоритмов решения показательных уравнений — привели обе части равенства к одинаковым основаниям. Дальше рассмотрим и другие методы.

Как решать уравнения с дробями

Универсальный алгоритм решения

Определить область допустимых значений.                  Найти общий знаменатель.                  Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.                  Раскрыть скобки, если нужно и привести подобные слагаемые.                  Решить полученное уравнение.                  Сравнить полученные корни с областью допустимых значений.                  Записать ответ, который прошел проверку.

А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

Как решаем:

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
      
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

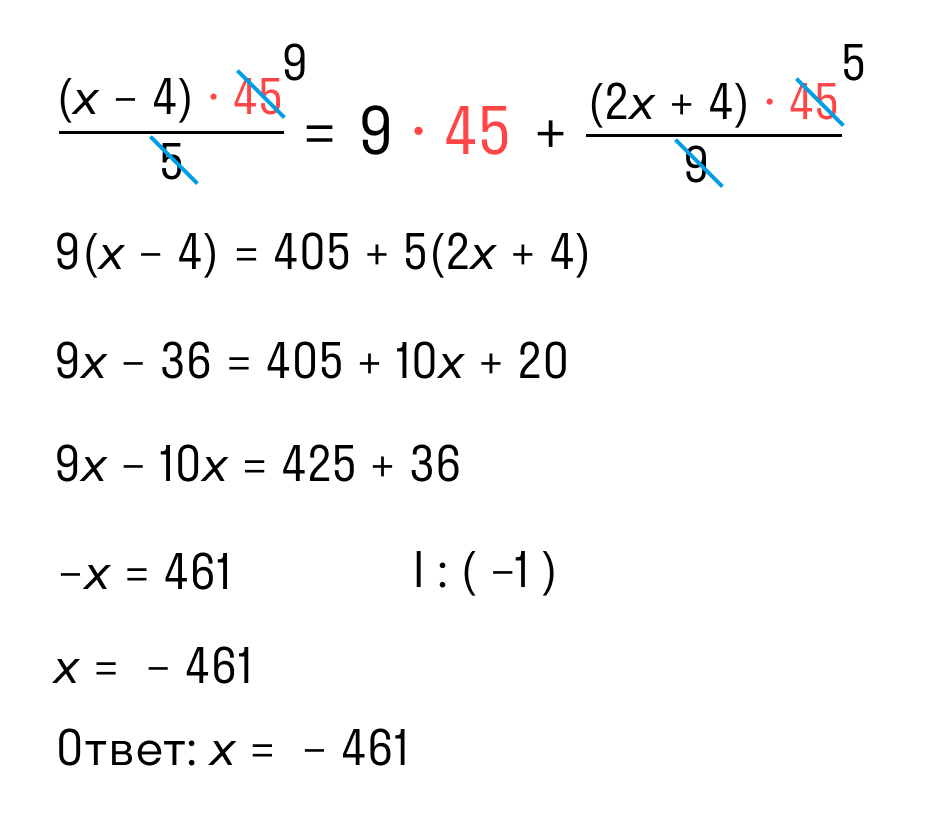
Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении
            
                
если значение переменной обращает знаменатель в 0, значит это неверное значение;
                
делить и умножать уравнение на 0 нельзя.
            

            

А вот и полезные видео для закрепления материала:

• уравнения с дробями 5 класс;
      
• уравнения с дробями 6 класс;
      
• уравнения с дробями 7 класс;

Учет ОДЗ

Помнишь, что такое ОДЗ?

Например, в уравнении \( \displaystyle \sqrt{x+2}=3\) присутствует квадратный корень. А квадратный корень не имеет смысла, если подкоренное выражение отрицательно. То есть, в данном случае ОДЗ – это решения неравенства \( \displaystyle x+2\ge 0\).

Нет необходимости искать ОДЗ в каждой задаче, содержащей корень.

Взять, например, задачу из предыдущей главы:

\( \displaystyle \sqrt{{{x}^{2}}+3x}=2\).

При возведении в квадрат получаем \( \displaystyle {{x}^{2}}+3x=4\), то есть подкоренное выражение автоматически неотрицательно! Так зачем лишняя писанина?

Но в некоторых случаях это может быть очень полезно. Более того, иногда можно решить пример, просто найдя ОДЗ!

Простейшие иррациональные уравнения

Начнем с самого простого: уравнения вида \( \displaystyle \sqrt{x}=a\).

Например: \( \displaystyle \sqrt{x}=3\). Как его решить? Как избавиться от корня? Правильно, квадратный корень убирается возведением в квадрат:

\( \displaystyle \sqrt{x}=3\text{ }\Leftrightarrow \text{ }{{\left( \sqrt{x} \right)}^{2}}={{3}^{2}}\text{ }\Leftrightarrow \text{ }x=9\).

А как решить такое: \( \displaystyle \sqrt{x}=3\)?

И снова вспомним определение корня степени \( \displaystyle n\): \( \displaystyle \sqrt{x}\) – это такое число, которое нужно возвести в степень \( \displaystyle n\), чтобы получить \( \displaystyle x\). В данном случае эта степень равна \( \displaystyle 3\):

Итак, общее правило:

Хорошо, а что с этим: \( \displaystyle \sqrt{{{x}^{2}}}=4\)? Все просто: квадрат и корень уничтожаются, и получаем \( \displaystyle x=4\), верно?

Нет! Когда мы проходили корни, на это обращали особое внимание: здесь два корня – \( \displaystyle x=4\) и \( \displaystyle x=-4\), ведь \( \displaystyle \sqrt{{{\left( -4 \right)}^{2}}}=\sqrt{16}=4\). Не забываем правило:

Не забываем правило:

Реши сам:

Замена переменной

Этот способ решения показательных уравнений понадобится тем, кто не боится по-настоящему трудных задач. Ведь с помощью ввода новой переменной можно упростить даже самое сложное выражение. Его суть проста: мы заменяем «трудную» переменную на более простую и решаем уравнение, а после производим обратную замену. Главное — определить, какую именно переменную стоит заменить.

Пример

4x- 2x+1- 8 = 0

Очевидно, что в этом уравнении показательные функции легко привести к общему основанию: 4х = 22х, а 2х+1 = 2 × 2х.

22х – 2 × 2х – 8 = 0

Что-то напоминает. Если бы из этого выражения можно было волшебным образом убрать 2х, получилось бы обычное квадратное уравнение. Поэтому мы обозначим 2х новой переменной — допустим, y.

Если 2х = y, получается: у2- 2у – 8 = 0.

У такого уравнения есть два корня: у₁ = 4, у₂ = -2.

Проведем обратную замену: 2х = 4, 2х = -2.

Но мы знаем, что показательная функция в любом случае не может быть отрицательным числом, а значит, 2х = -2 корней не имеет. Следовательно, 2х = 4.

х = 2.

Пример 2

25х – 6 × 5х + 5 = 0

Если присмотреться к этому выражению, становится понятно, что у него много общего с квадратным уравнением. Введем новую переменную: 5х = у.

у2 – 6у + 5 = 0

Корни такого уравнения: 1 и 5.

Выполним обратную замену:

5х = 1, значит х = 0.

5х = 5, значит х = 1.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

x2 = 16 не равно  x = √16.

Это два нетождественных друг другу выражения.

• x2 = 16 — это квадратное уравнение.
• x = √ 16 — арифметический квадратный корень.

Из выражения x2 = 16 следует, что:

|x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

1. Пример решен неверно
2. Это квадратное уравнение.

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения: 

1. x2 = 36
2. x = √36

Первое выражение — квадратное уравнение. 

|x| = √36
x1 = +6
x2 = -6.

Второе выражение — арифметический квадратный корень. 

√36 = 6
x = 6.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей. 

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

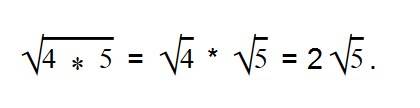
Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

1. √28
   Раскладываем подкоренное выражение на множители 28 = 7*4.
   Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.

2. Ответ: по правилу извлечения квадратного корня из произведения,
   Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.

3. Вынесите множитель из-под знака корня в выражении: √24
   Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.
4. Упростите выражение:
   Вынесем в двух последних выражения множитель из-под знака корня.
   Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.
   Мы видим, что во всем выражении есть один общий множитель — √5.
   Выносим общий множитель за скобки:
   Далее вычисляем все, что в скобках:

Решение дробно-рациональных уравнений

До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.

Приведем несколько примеров ур-ний, считающихся дробно-рациональными:

С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:

Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.

Обычно для решения дробно-рациональных уравнений используют такой алгоритм:

1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.

2) Решают полученное целое ур-ние.

3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.

Пример. Решите ур-ние

Решение.

Умножим обе части равенства на знаменатель 1-ой дроби:

2х2 – 3х – 2 = х2(х – 2)

Раскроем скобки и перенесем все слагаемые в одну сторону:

2х2 – 3х – 2 = х3– 2х2

х3 – 2х2 – 2х2 + 3х + 2 = 0

х3 – 4х2 + 3х + 2 = 0

У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:

23 – 4•22 + 3•2 + 2 = 8 – 16 + 6 + 2 = 0

Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):

Получили, что х3 – 4х2 + 3х + 2 = (х – 2)(х2 – 2х – 1)

Тогда ур-ние примет вид:

(х – 2)(х2 – 2х – 1) = 0

х – 2 = 0 или х2 – 2х – 1 = 0

Решим квадратное ур-ние:

D =b2 – 4ас = (– 2)2 – 4•1•(– 1) = 4 + 4 = 8

Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии

в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:

х – 2 = 2 – 2 = 0

Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.

Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:

Пример. Найдите все корни ур-ния

Решение. Если сразу привести выражение слева к общему знаменателю 4(х2 + х – 2)(х2 + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х2 + х как у:

у = х2 + х

Тогда уравнение примет вид

Приведем дроби к общему знаменателю 4(у – 2)(у – 20):

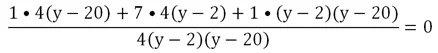
Знаменатель должен равняться нулю:

4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0

4у – 80 + 28у – 56 + у2 – 20у – 2у + 40 = 0

у2 + 10у – 96 = 0

Решаем квадратное ур-ние:

D =b2 – 4ас = (10)2 – 4•1•(– 96) = 100 + 384 = 484

Получили, что у₁ = – 16, а у₂ = 6. Произведем обратную замену:

у = х2 + х

х2 + х = – 16 или х2 + х = 6

х2 + х + 16 = 0 или х2 + х – 6 = 0

Дискриминант 1-ого ур-ния отрицателен:

D =b2 – 4ас = (1)2 – 4•1•(16) = 1– 64 = – 63

А потому оно не имеет решений. Решим 2-ое ур-ние:

D = b2 – 4ас = (1)2 – 4•1•(– 6) = 1+ 24 = 25

Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии

в ноль. Подстановкой можно убедиться, что не обращают.

Ответ: – 3 и 2.

При решении дробно-рациональных ур-ний может использоваться и графический метод.

Пример. Сколько корней имеет уравнение

Решение. Построим графики функций у = х2 – 4 и у = 2/х:

Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.

Ответ: 3 корня.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax2 + c = 0, при b = 0;
• ax2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.

Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6×2 = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6×2 = 0

   x2 = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:

• перенесем c в правую часть: ax2 = – c,
• разделим обе части на a: x2 = – c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x2 = – c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = – c/а не является верным.

Если — c/а > 0, то корни уравнения x2 = – c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = – c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = – c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению ax2 + c = 0, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8×2 + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8×2 = – 5

2. Разделим обе части на 8:

   x2 = – 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8×2 + 5 = 0 не имеет корней.

Как решить уравнение ax2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5×2 + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = 0,125,
   х = 0,125/0,5

4. Разделить:

   х = 0,25

5. Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Извлечение корней из больших чисел

До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!

Можно было пойти по иному пути и разложить на другие множители:

Что дальше? А дальше раскладываем на множители до самого конца:

Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.

Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:

Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:

А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):

Разве это конец? Не останавливаемся на полпути!

На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:

Вот и все, не так все и страшно, правда?

Получилось \( \displaystyle   90\)? Молодец, все верно!

А теперь попробуй вот такой пример решить:

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Что такое арифметический квадратный корень

А почему же число  \( a\) (число под корнем) должно быть обязательно неотрицательным?

Например, чему равен \( \sqrt{-9}\)?

Так-так, попробуем подобрать. Может, три?

Проверим: \( {{3}^{2}}=9\), а не \( -9\).

Может, \( \left( -3 \right)\)? 

Опять же, проверяем: \( {{\left( -3 \right)}^{2}}=9\).

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!

Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!

 Ведь в определении сказано, что «квадратным корнем из числа\( a\)называется такое неотрицательное число, квадрат которого равен\( a\)».

Но подождите!  В самом начале мы разбирали пример \( {{x}^{2}}=4\) и один из ответов был отрицательным числом! 

 Мы подбирали числа, которые можно возвести в квадрат и получить при этом \( \displaystyle 4\). Ответом были \( \displaystyle 2\) и \( \displaystyle -2\)

А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?

Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.

К примеру, \( \displaystyle {{x}^{2}}=4\) (квадратное уравнение) не равносильно выражению \( x=\sqrt{4}\) (арифмитический квадратный корень).

Из \( {{x}^{2}}=4\) следует, что

\( \left| x \right|=\sqrt{4}\), то есть \( x=\pm \sqrt{4}=\pm 2\) или \( {{x}_{1}}=2\); \( {{x}_{2}}=-2\)

(не помнишь почему так? Почитай тему «Модуль числа»!)

А из \( x=\sqrt{4}\) следует, что \( x=2\).

Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как \( 2\), так и \( x=-2\).

Приведение к одинаковому основанию

Весомую часть уравнений вида ах = b (при а и b 0) можно решить, превратив b в определенную степень числа a. Именно это мы сделали в примере выше, получив одинаковые основания. Главная трудность в том, чтобы найти у этих чисел общий множитель.

Если у нас есть одинаковые основания, но разные показатели степени, то при умножении чисел степени складываются, а при делении — вычитаются.

Пример 1

Рассмотрим еще одно показательное уравнение с корнем.

(1/642)-х = √1/8

Мы знаем, что у 64 и 8 есть общий множитель — это 2. Попробуем использовать это, и тогда 642 = 212, а 8 = 23.

(1/212)-х = √1/23

1/2-12х = 1/22/3

(1/2)-12х = (1/2)3/2

-12х = 3/2

х = -1/8

Пример 2

В этом примере показательного уравнения нужно будет отдельно преобразовать каждую составляющую.

(0,5)х2 × 4х+1 = 64-1

Найдем общее основание показательных функций:

0,5 = 1/2 = 2-1

4 = 22

64 = 26

В результате у нас получается:

(2-1)х2 × (22)х+1 = (26)-1

2-х2 × 22х+2 = 2-6

2-х2+2х+2 = 2-6

-х2 + 2х + 2 = -6

х2- 2х – 8 = 0

Здесь у нас будет два корня: -2 и 4.

Правила уменьшения или увеличения уравнения в несколько раз.

Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.

Рассмотрим пример:
Решите уравнение 5x=20.

Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.

5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4

Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.

Рассмотрим следующий пример:
Найдите корни уравнения   .

Решение:
Так как перед переменной x стоит коэффициент  необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.

1x=21 или x=21

Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.

7=7 получено верное равенство.

Ответ: корень уравнения равен x=21.

Следующий пример:
Найдите корни уравнения

Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а   в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте  перед переменной x убрать из знаменателя 5.

3x=45

Далее делим все уравнение на 3.

3x:3=45:3
(3:3)x=15

1x=15 или x=15

Сделаем проверку. Подставим в уравнение найденный корень.

5=5

Ответ: x=15

История и формулировки

Кубические уравнения составлялись ещё в Древней Греции и Египте. Археологами были найдены клинописные таблицы XVI века до нашей эры, содержащие описание возможного их решения. Вычислением кубов занимался Гиппократ, пытавшийся свести задачу к нахождению отрезков с помощью чертёжных инструментов. Архимед использовал для поиска ответа пересечение двух конусов.

Впервые методы решения такого рода уравнений были описаны в китайском учебнике «Математика в девяти книгах», составленном во втором столетии до нашей эры. В седьмом веке Омар Хайям на основании своих работ приходит к выводу, что решение уравнений третьей степени может иметь более одного ответа.

Математик Шараф ад-Дин публикует тракт об уравнениях, в котором описывает восемь различных типов кубических выражений, имеющих положительное решение. В своих вычислениях он использует численную аппроксимацию

Учёный не только разработал подход для решения с использованием производной функции и экстремумов, но и понял важность дискриминанта многочлена при нахождении кубов

В 1530 году итальянский математик Никколо Тарталья разрабатывает методику решения, которой он после поделился с Джероламо Кардано. Согласно этому способу нужно было извлекать квадратный корень из отрицательного числа. Параллельно с этими исследованиями, основоположник символической алгебры Франсуа Виет, предлагает свой способ решения кубического равенства с тремя корнями. Позднее его работу описал и обосновал Рене Декарт.

Уравнением третьей степени называют выражение вида: a*y 3 + d*y 2 + c*y + n = 0. В математике оно называется кососимметрическим. Число y, значение которого необходимо найти, при подстановке превращает формулу в тождество. Называется оно корнем уравнения или просто решением. Кроме этого, y ещё является и корнем многочлена куба.