Как найти сумму корней уравнения

Что называют теоремой?

Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.

Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.

Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.

Например, теоремой можно назвать следующее утверждение:

«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».

А затем привести такое доказательство:

Пусть, имеется дробь . Умнóжим числитель и знаменатель этой дроби на число с. Тогда полýчится дробь . Докáжем, что дроби  и равны. То есть докажем, что равенство является верным.

Для доказательства этого равенства воспользуемся основным свойством пропорции:

От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:

Поскольку равенство является пропорцией, а пропорция это равенство двух отношений, то дроби и равны. Теорема доказана.

Правила уменьшения или увеличения уравнения в несколько раз.

Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.

Рассмотрим пример:
Решите уравнение 5x=20.

Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.

5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4

Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.

Рассмотрим следующий пример:
Найдите корни уравнения   .

Решение:
Так как перед переменной x стоит коэффициент  необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.

1x=21 или x=21

Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.

7=7 получено верное равенство.

Ответ: корень уравнения равен x=21.

Следующий пример:
Найдите корни уравнения

Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а   в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте  перед переменной x убрать из знаменателя 5.

3x=45

Далее делим все уравнение на 3.

3x:3=45:3
(3:3)x=15

1x=15 или x=15

Сделаем проверку. Подставим в уравнение найденный корень.

5=5

Ответ: x=15

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax2 + c = 0, при b = 0;
• ax2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.

Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6×2 = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6×2 = 0

   x2 = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:

• перенесем c в правую часть: ax2 = – c,
• разделим обе части на a: x2 = – c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x2 = – c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = – c/а не является верным.

Если — c/а > 0, то корни уравнения x2 = – c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = – c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = – c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению ax2 + c = 0, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8×2 + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8×2 = – 5

2. Разделим обе части на 8:

   x2 = – 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8×2 + 5 = 0 не имеет корней.

Как решить уравнение ax2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5×2 + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = 0,125,
   х = 0,125/0,5

4. Разделить:

   х = 0,25

5. Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Квадратное уравнение и его корни. Неполные квадратные уравнения

Каждое из уравнений
\(-x^2+6x+1,4=0, \quad 8x^2-7x=0, \quad x^2-\frac{4}{9}=0 \)
имеет вид
\(ax^2+bx+c=0, \)
где x – переменная, a, b и c – числа.
В первом уравнении a = -1, b = 6 и c = 1,4, во втором a = 8, b = -7 и c = 0, в третьем a = 1, b = 0 и c = 4/9. Такие уравнения
называют квадратными уравнениями
.

Определение.Квадратным уравнением
называется уравнение вида ax 2 +bx+c=0, где x – переменная, a, b и c – некоторые числа,
причём \(a \neq 0 \).

Числа a, b и c – коэффициенты квадратного уравнения. Число a называют первым коэффициентом, число b – вторым коэффициентом и
число c – свободным членом.

В каждом из уравнений вида ax 2 +bx+c=0, где \(a \neq 0 \), наибольшая степень переменной x – квадрат. Отсюда и название:
квадратное уравнение.

Заметим, что квадратное уравнение называют ещё уравнением второй степени, так как его левая часть есть многочлен второй степени.

Квадратное уравнение, в котором коэффициент при x 2 равен 1, называют приведённым квадратным уравнением
.
Например, приведёнными квадратными уравнениями являются уравнения
\(x^2-11x+30=0, \quad x^2-6x=0, \quad x^2-8=0 \)

Если в квадратном уравнении ax 2 +bx+c=0 хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называют
неполным квадратным уравнением
. Так, уравнения -2x 2 +7=0, 3x 2 -10x=0, -4x 2 =0 – неполные
квадратные уравнения. В первом из них b=0, во втором c=0, в третьем b=0 и c=0.

Неполные квадратные уравнения бывают трёх видов:
1) ax 2 +c=0, где \(c \neq 0 \);
2) ax 2 +bx=0, где \(b \neq 0 \);
3) ax 2 =0.

Рассмотрим решение уравнений каждого из этих видов.

Для решения неполного квадратного уравнения вида ax 2 +c=0 при \(c \neq 0 \) переносят его свободный член в правую часть
и делят обе части уравнения на a:
\(x^2 = -\frac{c}{a} \Rightarrow x_{1,2} = \pm \sqrt{ -\frac{c}{a}} \)

Так как \(c \neq 0 \), то \(-\frac{c}{a} \neq 0 \)

Если \(-\frac{c}{a}>0 \), то уравнение имеет два корня.

Если \(-\frac{c}{a} Для решения неполного квадратного уравнения вида ax 2 +bx=0 при \(b \neq 0 \) раскладывают его левую часть на множители
и получают уравнение
\(x(ax+b)=0 \Rightarrow \left\{ \begin{array}{l} x=0 \\ ax+b=0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x=0 \\ x=-\frac{b}{a} \end{array} \right. \)

Значит, неполное квадратное уравнение вида ax 2 +bx=0 при \(b \neq 0 \) всегда имеет два корня.

Неполное квадратное уравнение вида ax 2 =0 равносильно уравнению x 2 =0 и поэтому имеет единственный корень 0.

Теорема, обратная теореме Виета

Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x₁ и x₂ равно свободному члену уравнения x2 + bx + c = 0, то числа x₁ и x₂ являются корнями уравнения x2 + bx + c = 0.

Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.

Так, доказывая теорему Виета мы пришли к заключению, что сумма x₁ и x₂ равна −b, а произведение x₁ и x₂ равно c. В обратной же теореме это заключение служит утверждением.

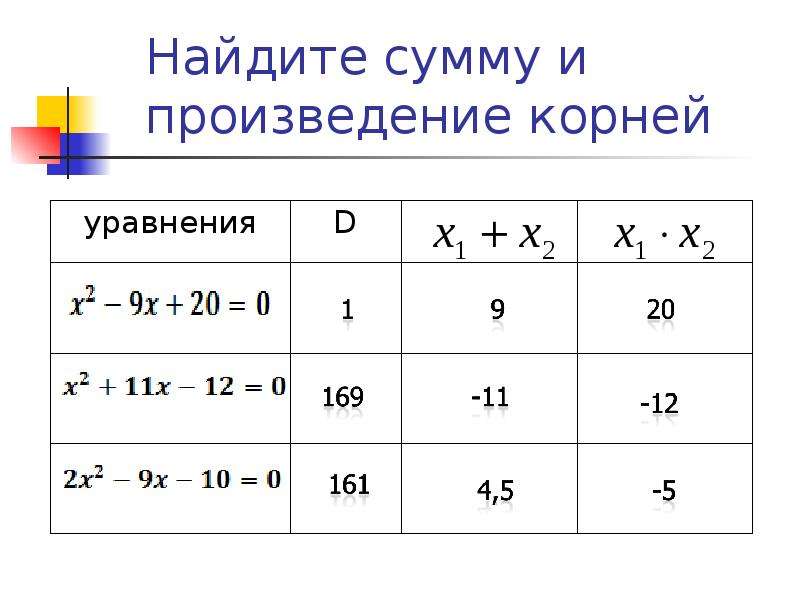
Ранее мы решили уравнение x2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:

А затем подобрали корни 3 и 2. По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x2 − 5x + 6 = 0, взятому с противоположным знаком (числу 5), а произведение чисел 3 и 2 равно свободному члену (числу 6). Значит числа 3 и 2 являются корнями уравнения x2 − 5x + 6 = 0.

Пример 2. Решить квадратное уравнение x2 − 6x + 8 = 0 по теореме, обратной теореме Виета.

В данном уравнении a = 1. Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.

Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6, поскольку второй коэффициент исходного уравнения равен −6. А произведение корней будет равно 8

Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x₁ + x₂ = 6, так и равенству x₁ × x₂ = 8

Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x₁ × x₂ = 8 нужно найти такие x₁ и x₂, произведение которых равно 8.

Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.

4 × 2 = 81 × 8 = 8

Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли не только равенству x₁ × x₂ = 8, но и равенству x₁ + x₂ = 6.

Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x₁ × x₂ = 8, но не удовлетворяют равенству x₁ + x₂ = 6.

Зато значения 4 и 2 подходят как равенству x₁ × x₂ = 8, так и равенству x₁ + x₂ = 6, поскольку эти значения удовлетворяют обоим равенствам:

Значит корнями уравнения x2 − 6x + 8 = 0 являются числа 4 и 2.

Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x₁ и x₂ обозначим как m и n. Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:

Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x2 + bx + c = 0, то числа m и n являются корнями уравнения x2 + bx + c = 0

Для начала запишем, что сумма m и n равна −b, а произведение mn равно c

Чтобы доказать, что числа m и n являются корнями уравнения x2 + bx + c = 0, нужно поочередно подстáвить буквы m и n в это уравнение вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x2 + bx + c = 0.

Помимо букв m и n нам нужно знать чему равен параметр b. Выразим его из равенства m + n = −b. Легче всего это сделать, умножив обе части этого равенства на −1

Теперь всё готово для подстановок. Подстáвим m в уравнение x2 + bx + c = 0 вместо x, а выражение −m − n подставим вместо b

Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x2 + bx + c = 0.

Аналогично докажем, что число n является корнем уравнения x2 + bx + c = 0. Подставим вместо x букву n, а вместо c подставим mn, поскольку c = mn.

Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.

Следовательно, числа m и n являются корнями уравнения x2 + bx + c = 0.

Понятие квадратного уравнения

Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac

А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Теорема, обратная теореме Виета

Вторая формулировка теоремы Виета, приведенная в предыдущем пункте, указывает, что если x 1
и x 2
корни приведенного квадратного уравнения x 2 +p·x+q=0
, то справедливы соотношения x 1 +x 2 =−p
, x 1 ·x 2 =q
. С другой стороны, из записанных соотношений x 1 +x 2 =−p
, x 1 ·x 2 =q
следует, что x 1
и x 2
являются корнями квадратного уравнения x 2 +p·x+q=0
. Иными словами, справедливо утверждение, обратное теореме Виета. Сформулируем его в виде теоремы, и докажем ее.

Теорема.

Если числа x 1
и x 2
таковы, что x 1 +x 2 =−p
и x 1 ·x 2 =q
, то x 1
и x 2
являются корнями приведенного квадратного уравнения x 2 +p·x+q=0
.

Доказательство.

После замены в уравнении x 2 +p·x+q=0
коэффициентов p
и q
их выражения через x 1
и x 2
, оно преобразуется в равносильное уравнение .

Подставим в полученное уравнение вместо x
число x 1
, имеем равенство x 1 2 −(x 1 +x 2)·x 1 +x 1 ·x 2 =0
, которое при любых x 1
и x 2
представляет собой верное числовое равенство 0=0
, так как x 1 2 −(x 1 +x 2)·x 1 +x 1 ·x 2 =
x 1 2 −x 1 2 −x 2 ·x 1 +x 1 ·x 2 =0
. Следовательно, x 1
– корень уравнения x 2 −(x 1 +x 2)·x+x 1 ·x 2 =0
, а значит, x 1
– корень и равносильного ему уравнения x 2 +p·x+q=0
.

Если же в уравнение x 2 −(x 1 +x 2)·x+x 1 ·x 2 =0
подставить вместо x
число x 2
, то получим равенство x 2 2 −(x 1 +x 2)·x 2 +x 1 ·x 2 =0
. Это верное равенство, так как x 2 2 −(x 1 +x 2)·x 2 +x 1 ·x 2 =
x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0
. Следовательно, x 2
тоже является корнем уравнения x 2 −(x 1 +x 2)·x+x 1 ·x 2 =0
, а значит, и уравнения x 2 +p·x+q=0
.

На этом завершено доказательство теоремы, обратной теореме Виета.

Как решать уравнения? Алгоритм действий.

Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:

1. Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
2. Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
3. Избавиться от коэффициента при переменной если нужно.
4. В итоге всех действий получаем корень уравнение. Выполняем проверку.

Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды)

Поэтому важно понять эти простые правила и научиться ими пользоваться.