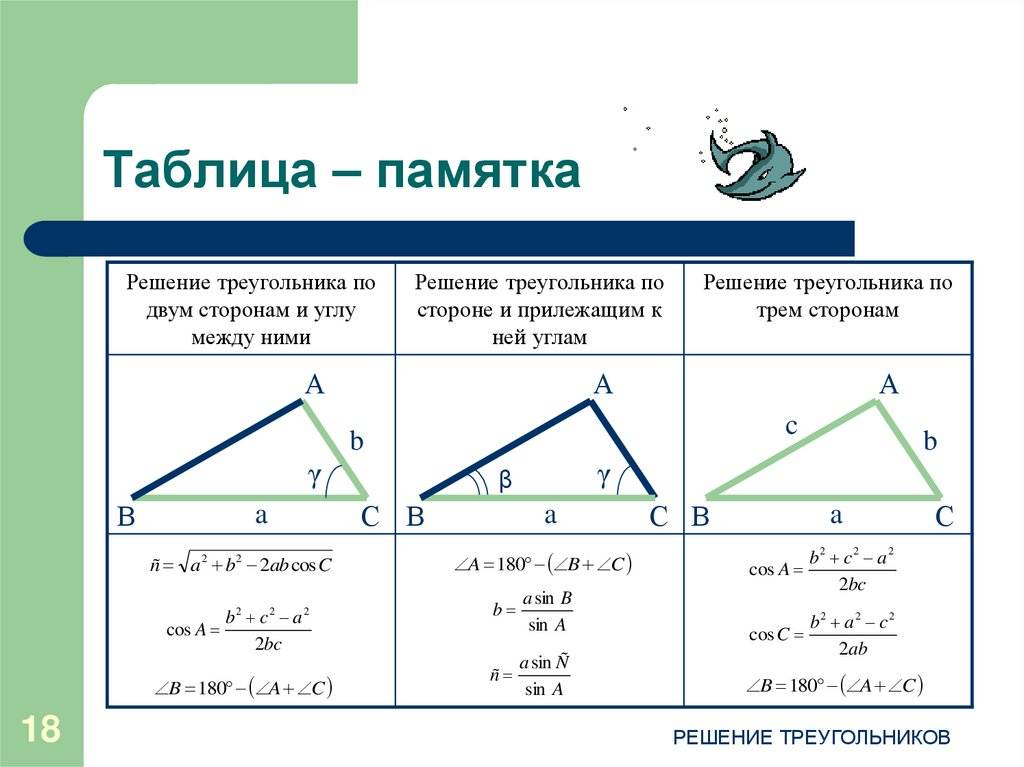
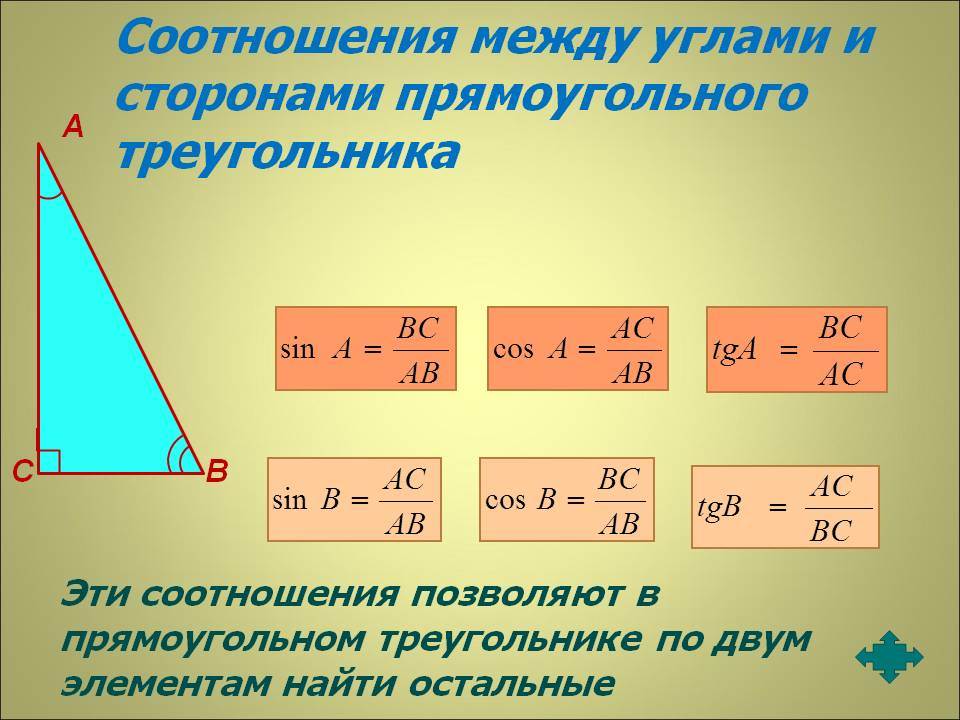
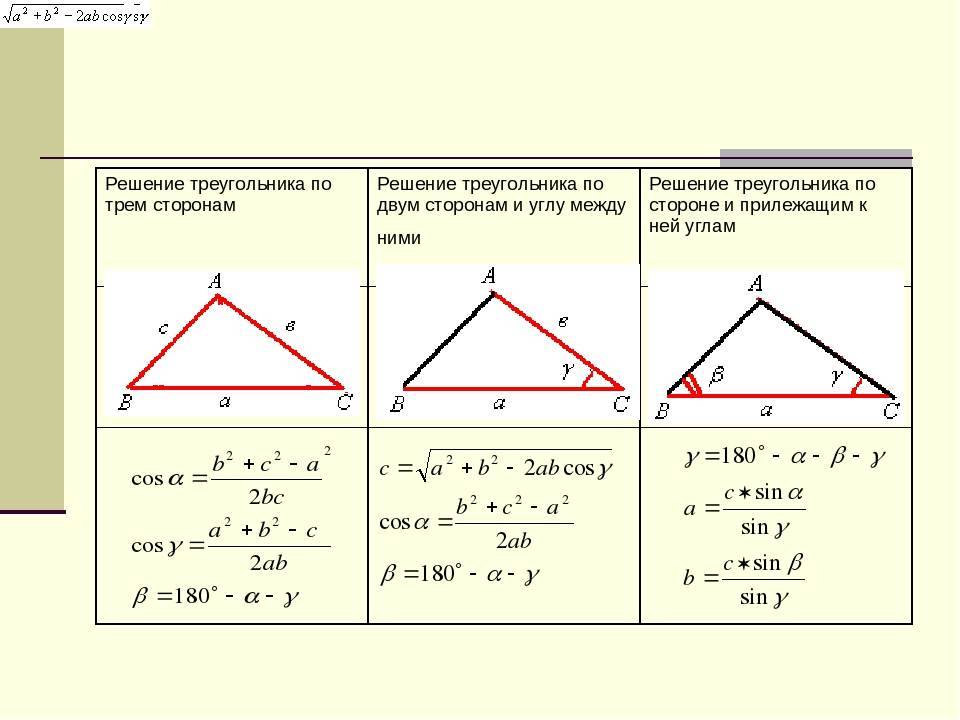
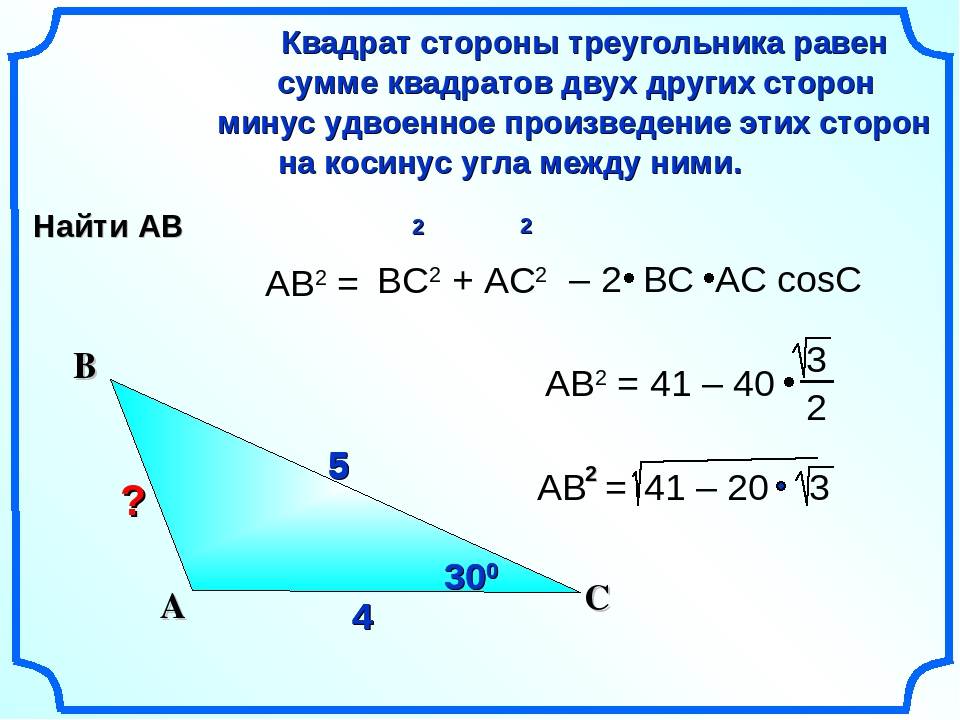
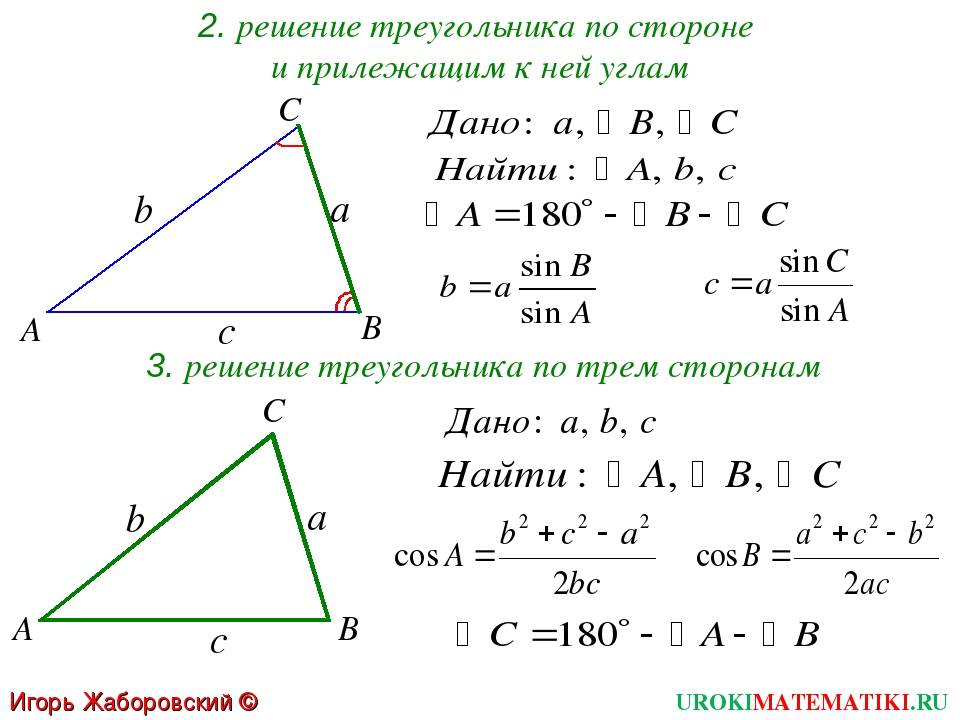
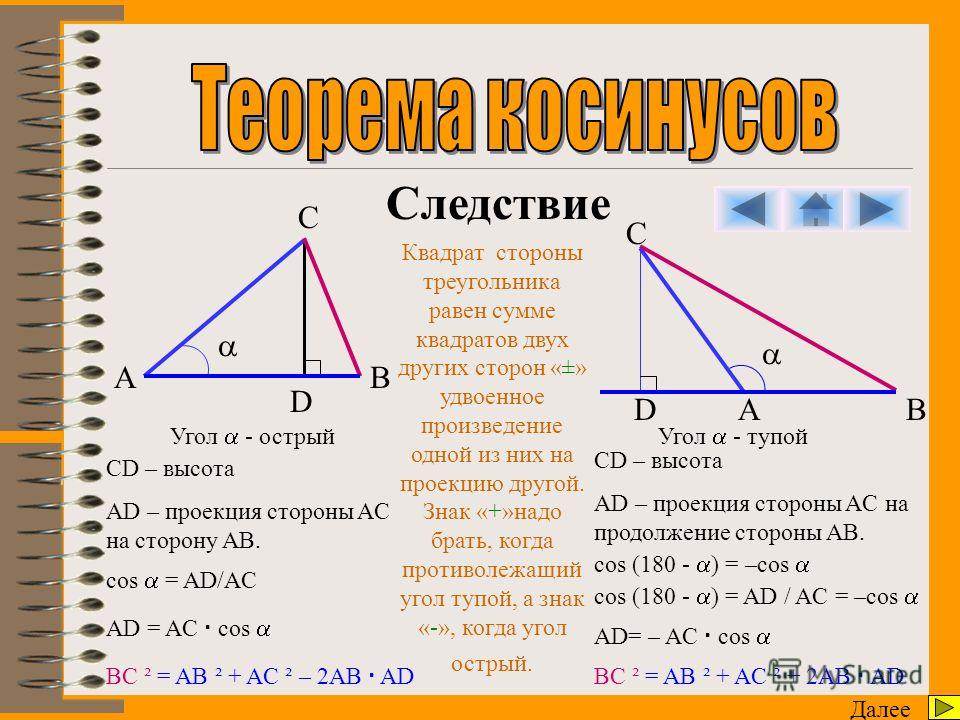
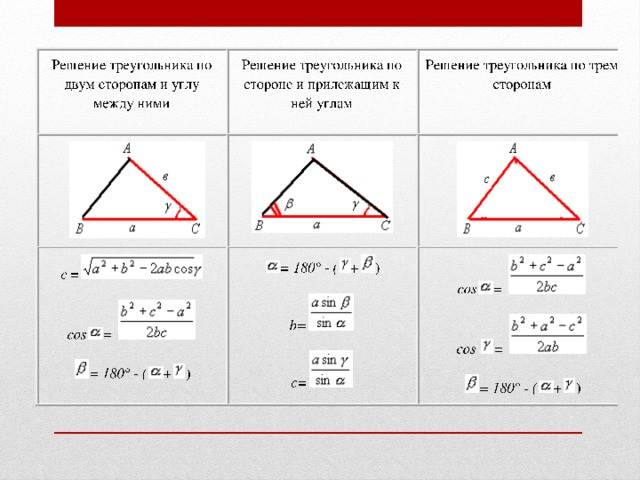
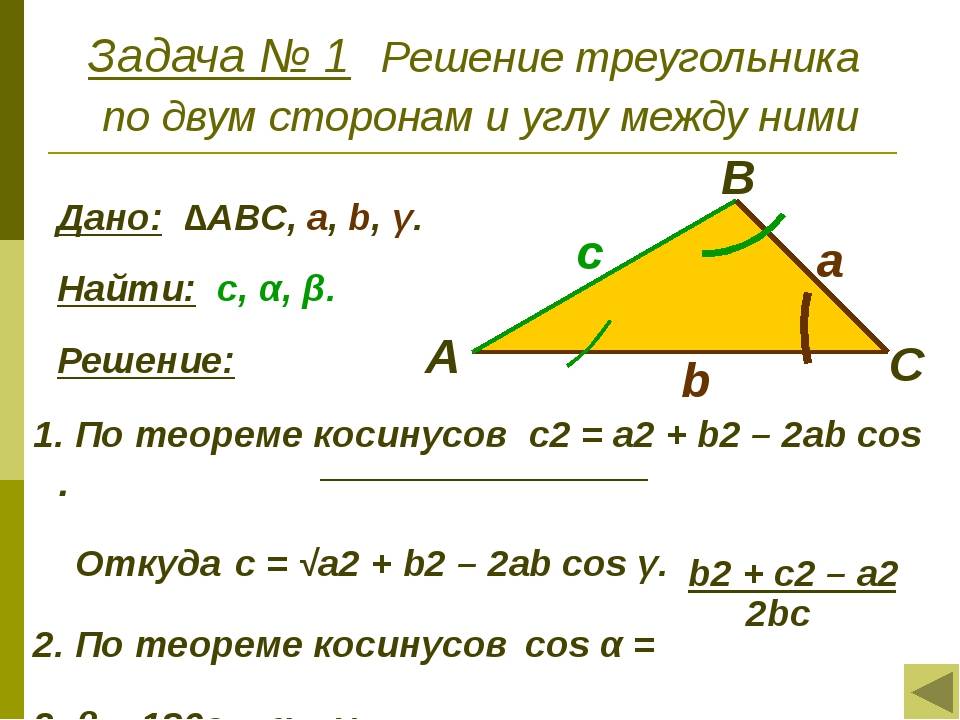
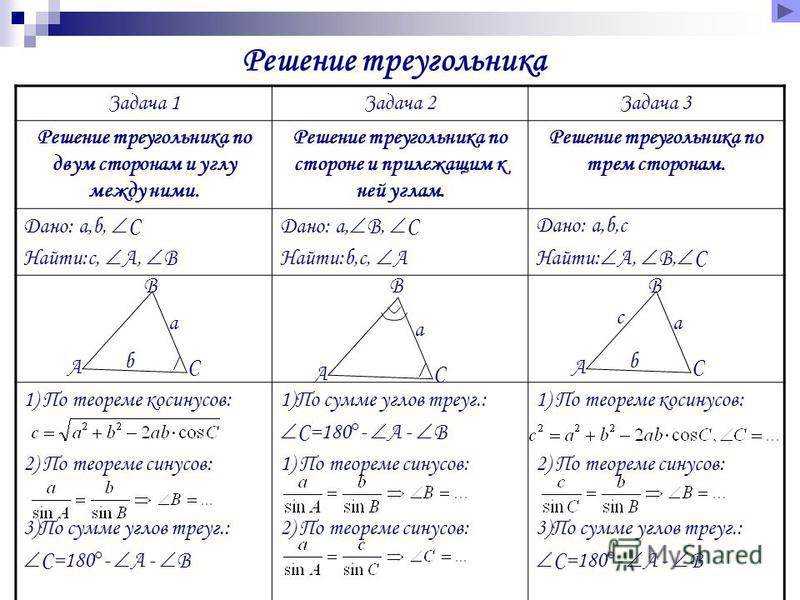
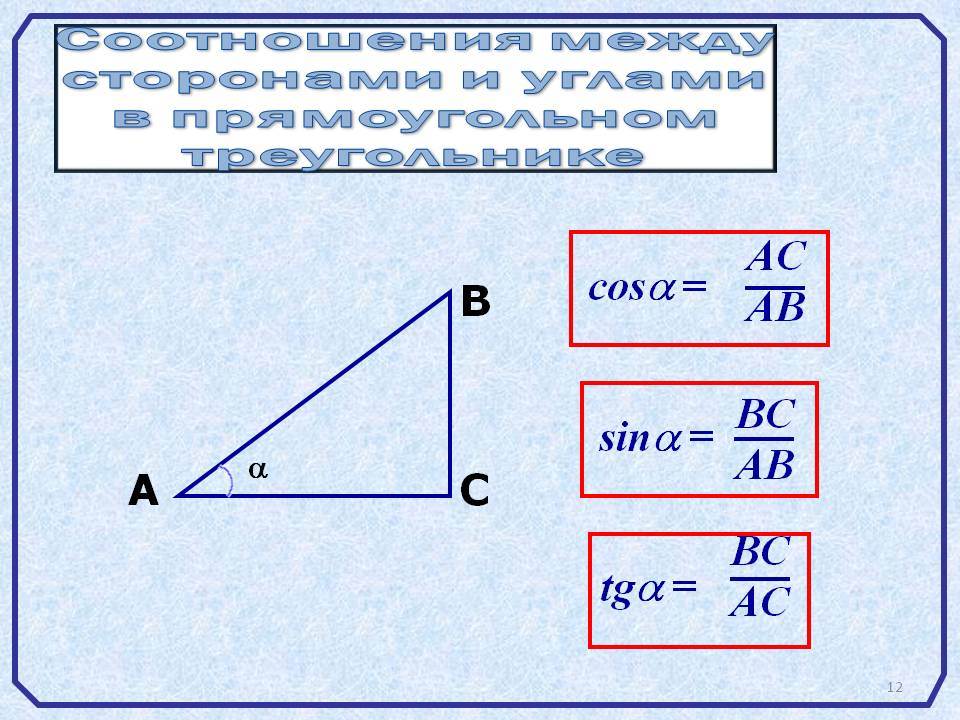
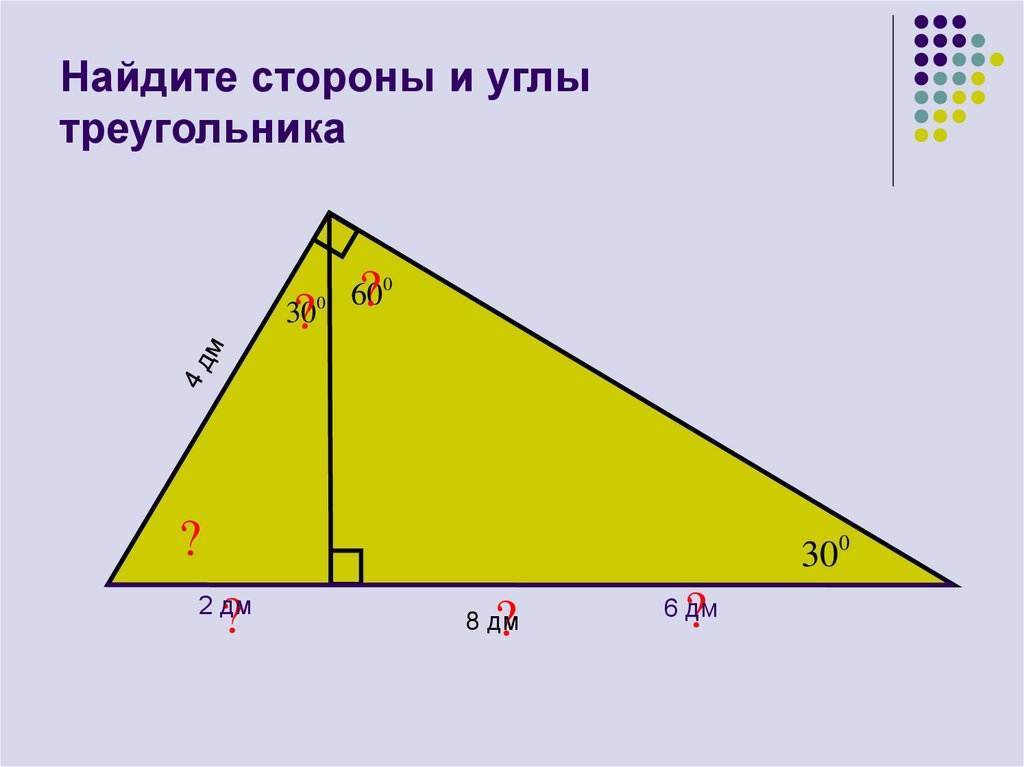
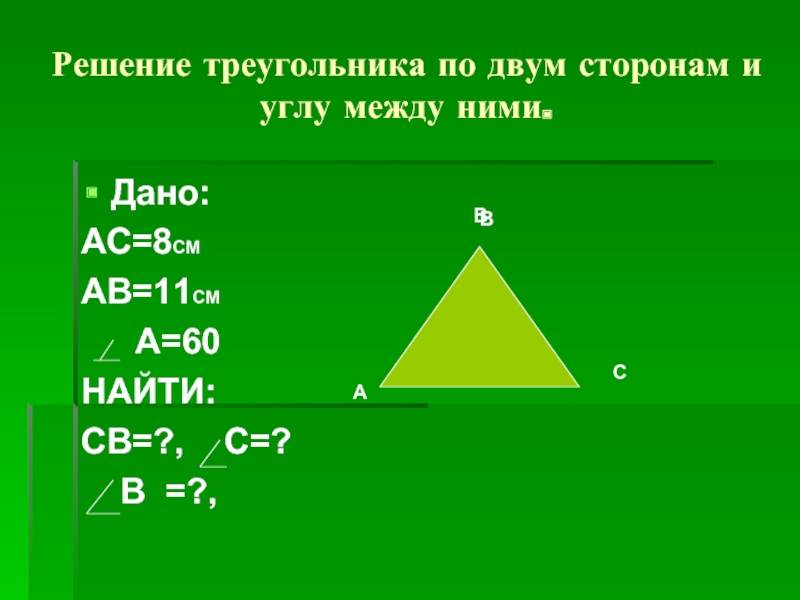
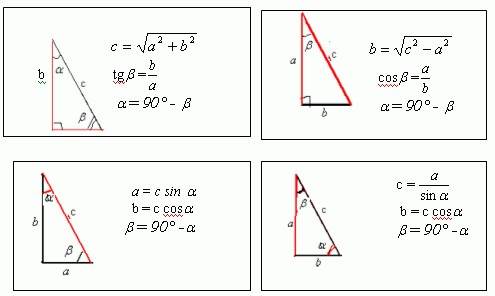
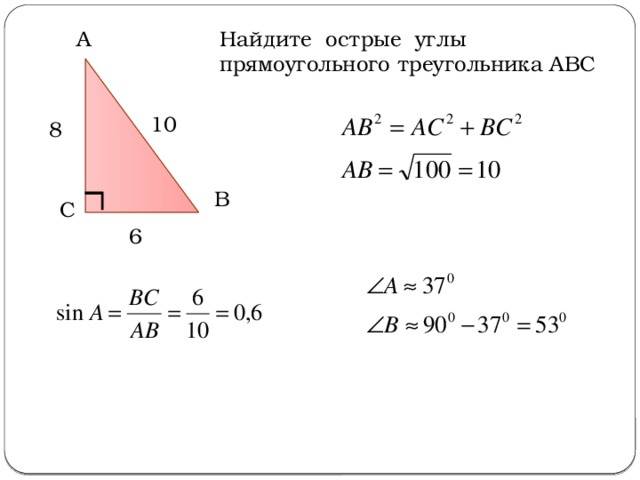
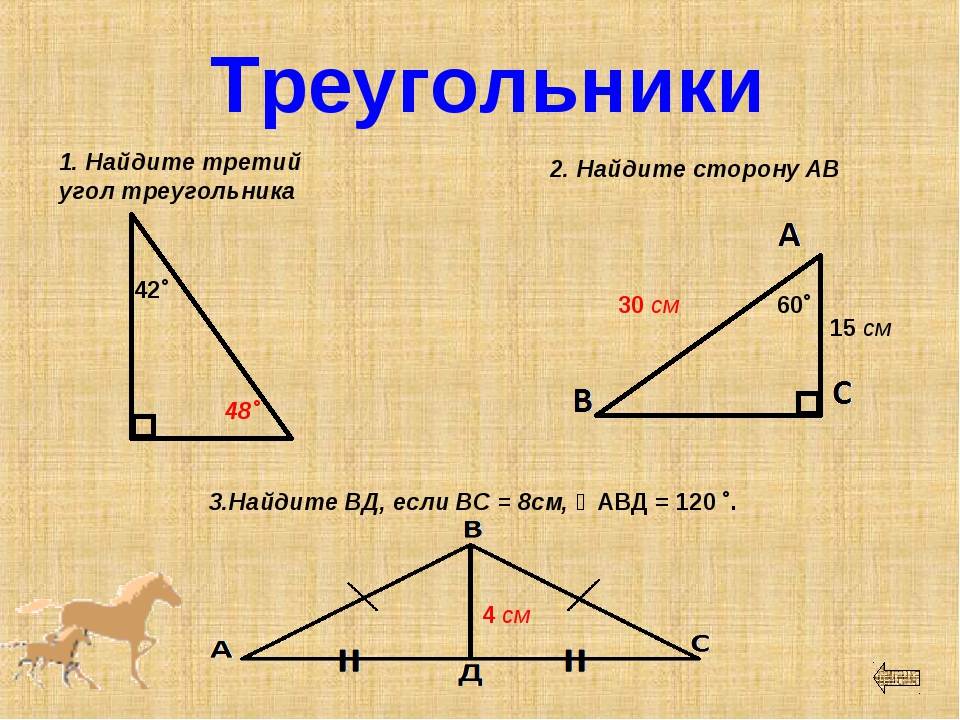
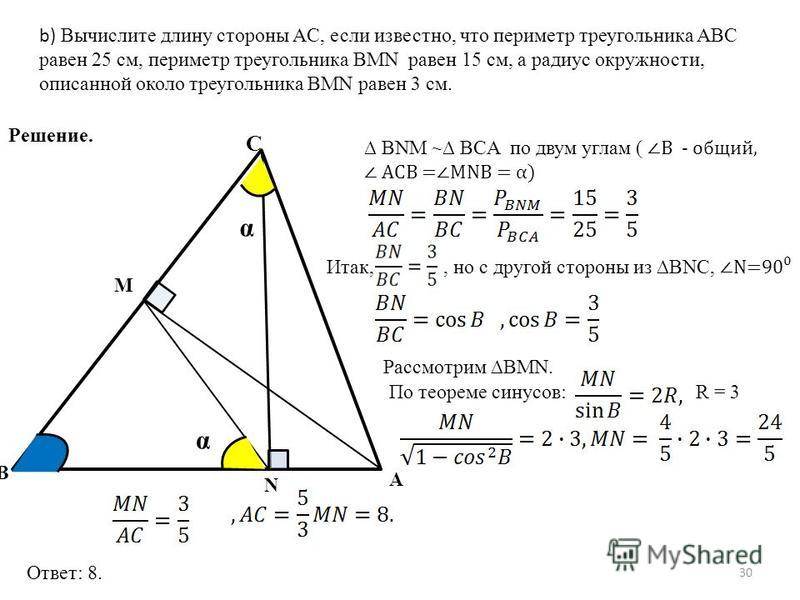
Как найти сторону треугольника, зная сторону и угол

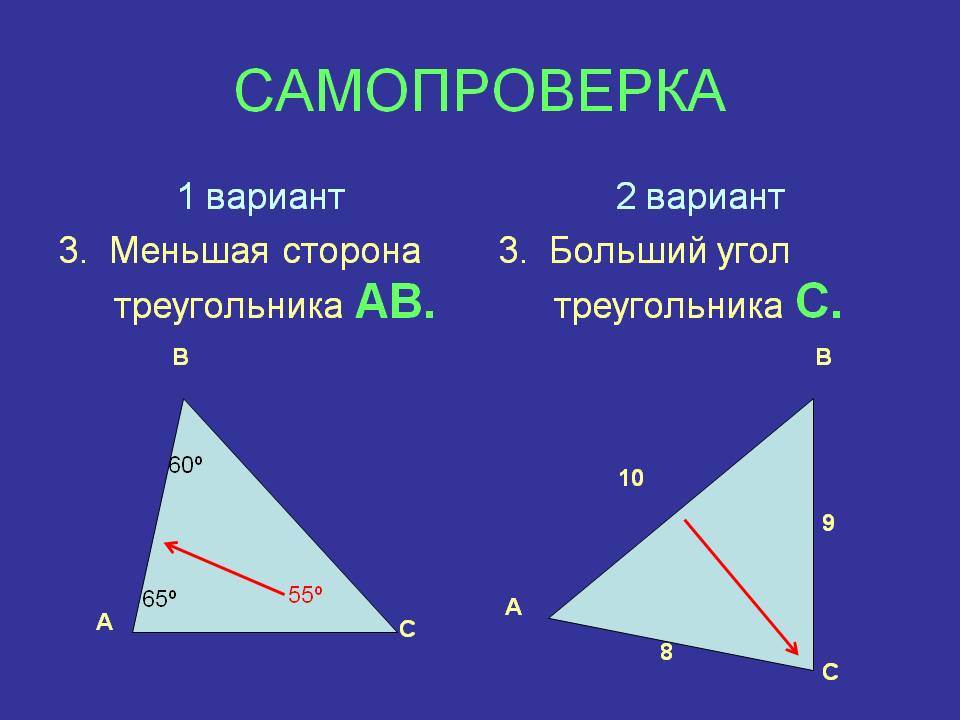
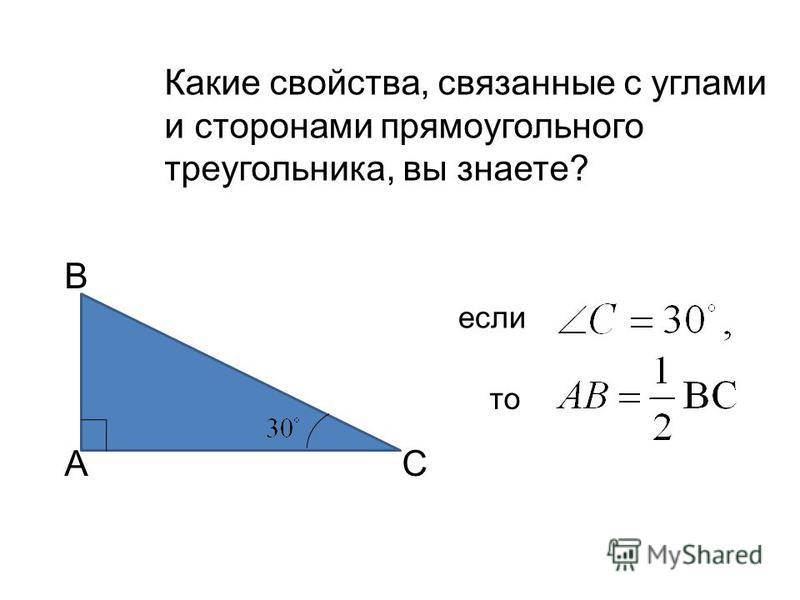
Способы нахождения длины стороны

Рассматриваемая фигура обладает достаточно большим количеством геометрических свойств, которые имеют математическое выражение в виде формул. Также для нее применимы особенности тригонометрических функций и общие формулы для треугольников общего типа. Весь этот набор равенств можно использовать для нахождения любой неизвестной стороны прямоугольной фигуры. Чаще всего встречаются задачи следующего типа:

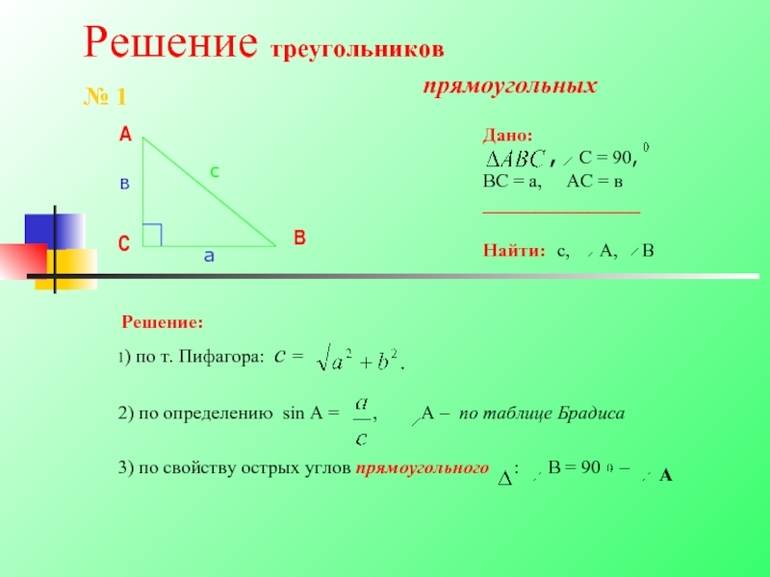
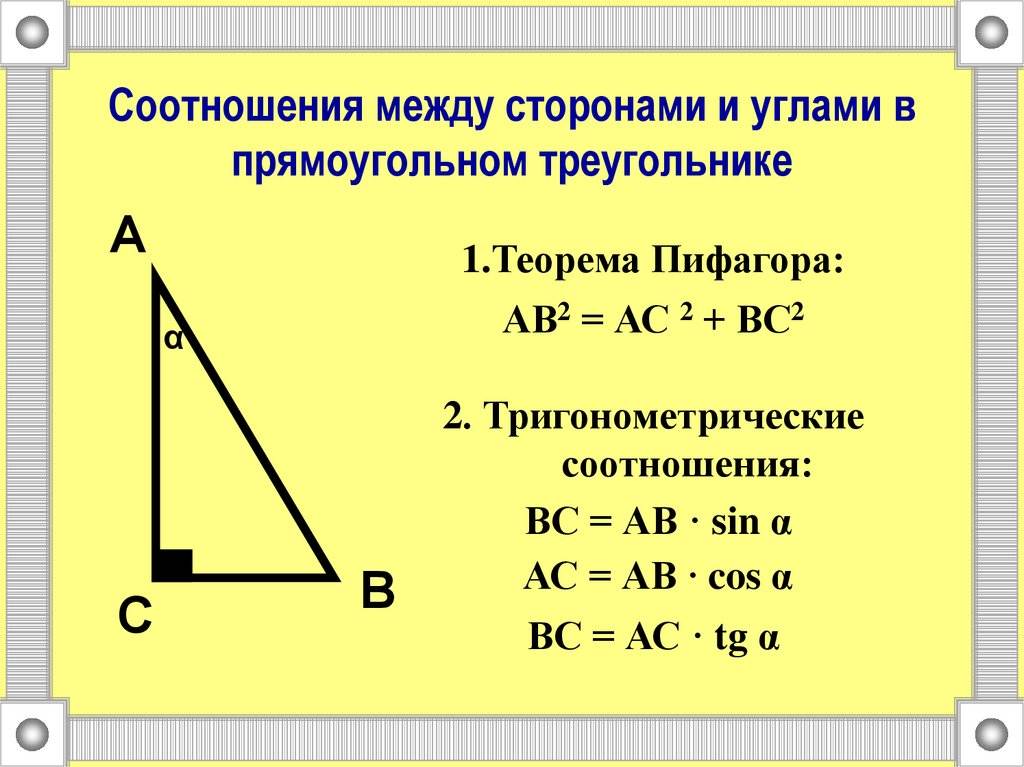
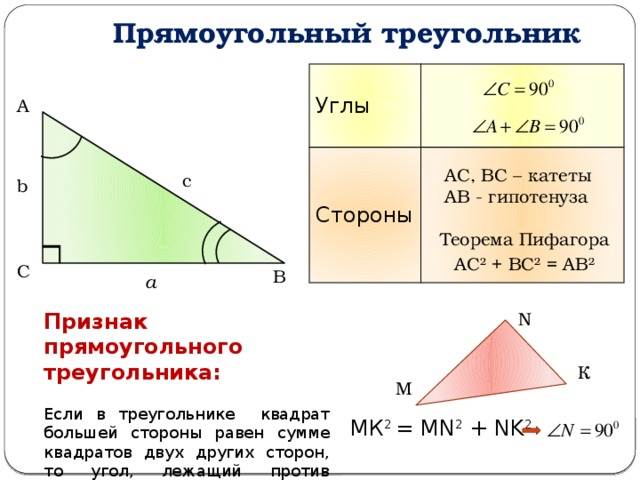
Известны две любые стороны. Независимо от того, неизвестен один из катетов или гипотенуза, найти эту сторону легко с использованием теоремы Пифагора. Пример для катета a выглядит так: a = (c 2 — b 2 )^0,5.
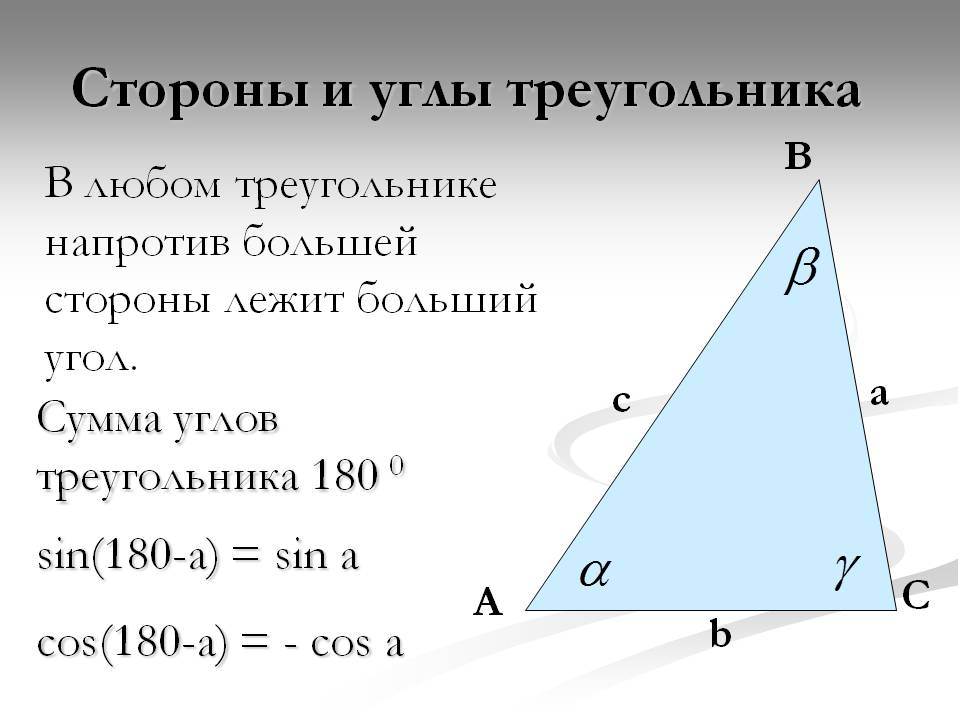
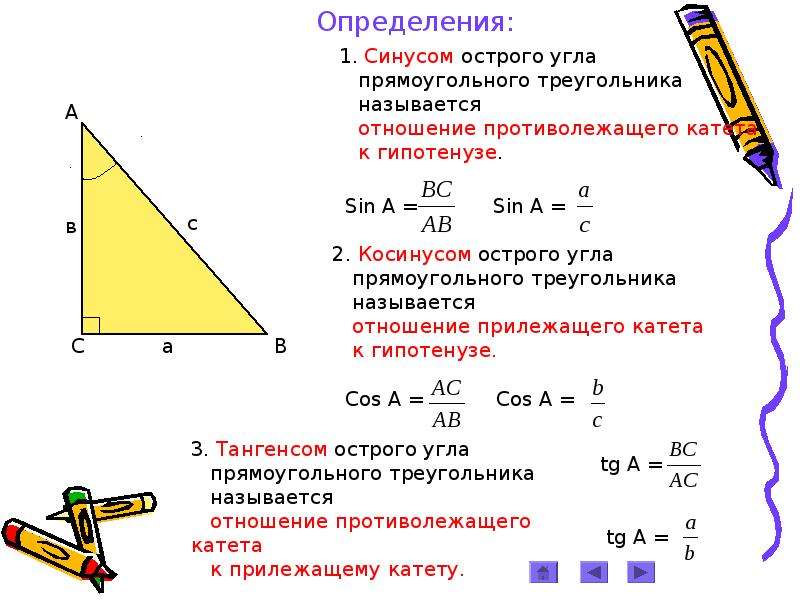
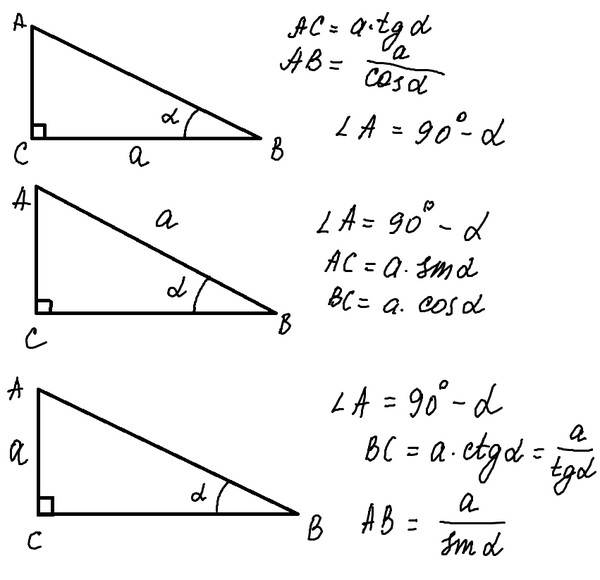
По известному острому углу и произвольной стороне. В этом случае любую из двух оставшихся неизвестных сторон треугольника легко вычислить с помощью соответствующей тригонометрической функции. Например, известен угол ∠ B и катет a, тогда: b = a*tgB, с = a/cosB.
По катету и высоте, проведенной из прямого угла. Для решения этой задачи сначала необходимо найти острый угол исходного треугольника, который определяется с помощью тригонометрической функции синуса. Как только он станет известен, задача сводится к типу 2.
По периметру и стороне. Эта задача имеет более сложный характер, чем описанные ранее. Решается она с помощью той же теорема Пифагора, но с применением теории квадратных уравнений.
Наконец, самый сложный вариант задачи на нахождение произвольного катета по известным площади фигуры и высоте, которая опущена из прямого угла. Здесь также необходимо использовать теорию решения квадратных уравнений, но в дополнение к этому следует использовать замену переменных.

Пусть площадь треугольника составляет 60 см 2 , а опущенная высота из острого угла равна 8 см. Необходимо посчитать, какие длины имеют катеты и гипотенуза.

Если внимательно прочитать условие задачи, то можно увидеть, что сама высота является одним из катетов, поскольку опущена она на основание не из прямого, а из острого угла. Пусть катет a = 8 см. Сторона b вычисляется по формуле для площади:

S = ½*a*b ==>

b = 2*S/a = 2*60/8 = 15 см.

Определить гипотенузу легко по формуле Пифагора:

c = (a 2 + b2)^0,5 = (82 + 152)^0,5 = 17 см.

Как найти стороны прямоугольного треугольника

Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

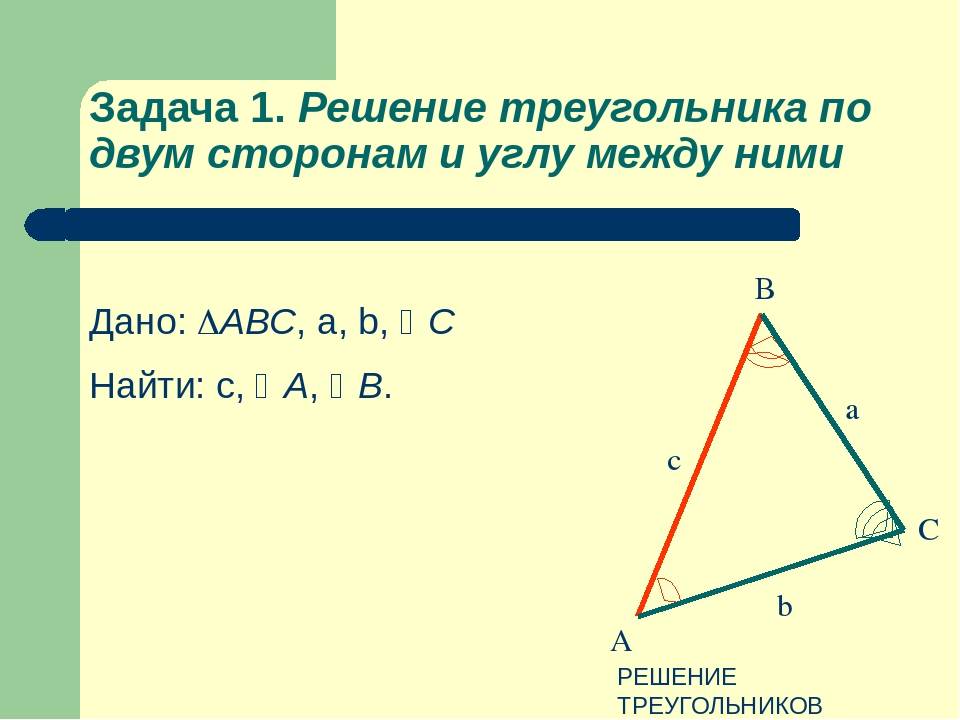
По двум сторонам и углу между ними. Параметры треугольника

Вы ввели следующие параметры треугольника

Рассчитанный треугольник и его свойства (в условных единицах)

Представляем небольшие калькуляторы основанные на универсальном решателе треугольников. Не все могут отыскать этот калькулятор, поэтому с помощью частных решений , мы предоставляем возможность узнавать параметры треугольника по двум сторонам и углу между ними.

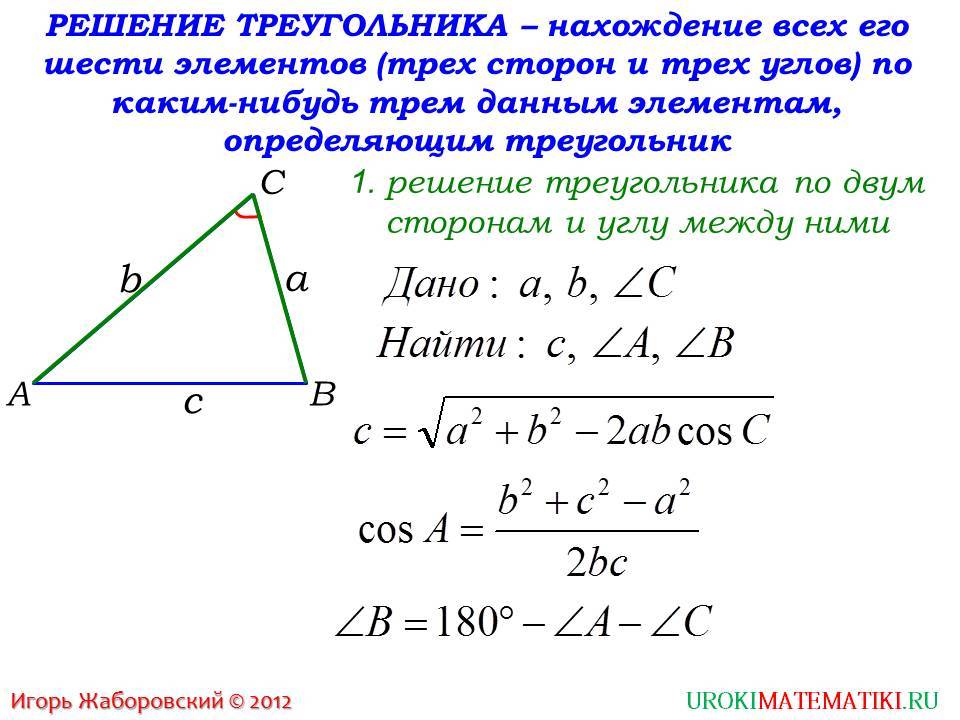
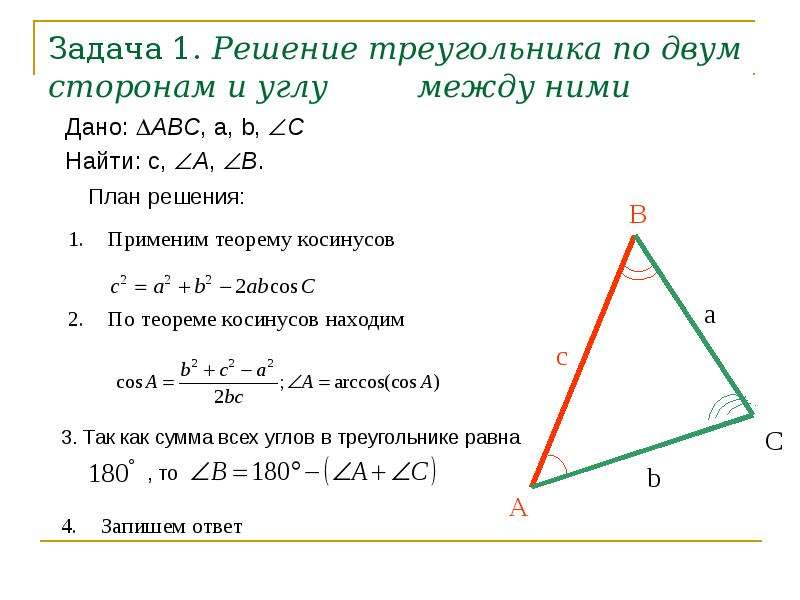
Итак, если у нас есть треугольник вида

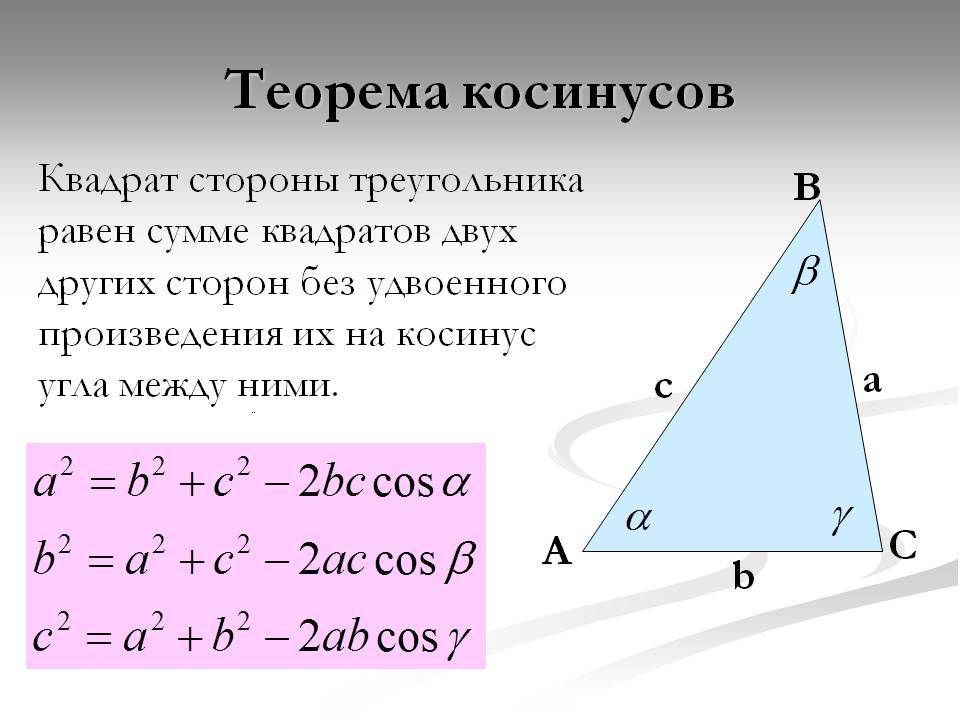
и известны строны a, b и угол между ними, то однозначно определяется неизвестная третья сторона, по формуле

Далее, можем по этой же формуле находить оставшиеся неизвестными два угла. Например для угла в точке A формула будет такой:

Бот, по заданным трем параметрам, выведет все рассчитанные значения в одной таблице.

Примеры решения:

Длина одной стороны 8 единиц, другой 14 единиц. Угол между ними 55 градусов.

Определить все возможные параметры треугольника.

В геометрии желательно или мысленно или на бумаге прорировать Ваш исходный треугольник, что бы Вы понимали что где находится и что надо найти. В противном случае, непонимание условия задачи влечет за собой неспособность её решить.

Как Вы обозначите стороны на своем рисунке неважно. Поэтому и поля ввода имеют свободный вид, то есть можно написать a=8 или с=8

Ввод же угла прост и вводится

Вы ввели следующие параметры треугольника

Рассчитанный треугольник и его свойства (в условных единицах)

A = 35.150232566068 B = 89.849767433932 C = 55 S = 45.872514480183 a = 8 b = 14 c = 11.468168042777 ha = 11.468128620045 hb = 6.5532163543118 hc = 7.9999724993696 ma = 12.155634048814 mb = 6.9827959392127 mc = 9.8549622239589 p = 16.734084021388

Еще один пример

Решим классическую задачу сторона a=4 сторона b=3 а угол межд ними 90 градусов

так и запишем. Получим ответ.

Вы ввели следующие параметры треугольника

Рассчитанный треугольник и его свойства (в условных единицах)

A = 53.130102354156 B = 36.869897645844 C = 90 S = 6 a = 4 b = 3 c = 5 ha = 3 hb = 4 hc = 2.4 ma = 3.605551275464 mb = 4.2720018726587 mc = 2.5 p = 6

Получили что это прямоугольный треугольник.

И напоследок.

Кто попал впервые на эту страницу смогут сразу не понять, что за обозначения означают те, или иные символы.

Ниже представлен список, для соответствия.

Сторона a

Сторона b

Сторона c

Полупериметр p

Угол А

Угол B

Угол C

Площадь треугольника S

Высота ha на сторону a

Высота hb на сторону b

Высота hc на сторону c

Медиана ma на сторону a

Медиана mb на сторону b

Медиана mc на сторону c

Координаты вершин (xa,ya) (xb,yb) (xc,yc)

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.

Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

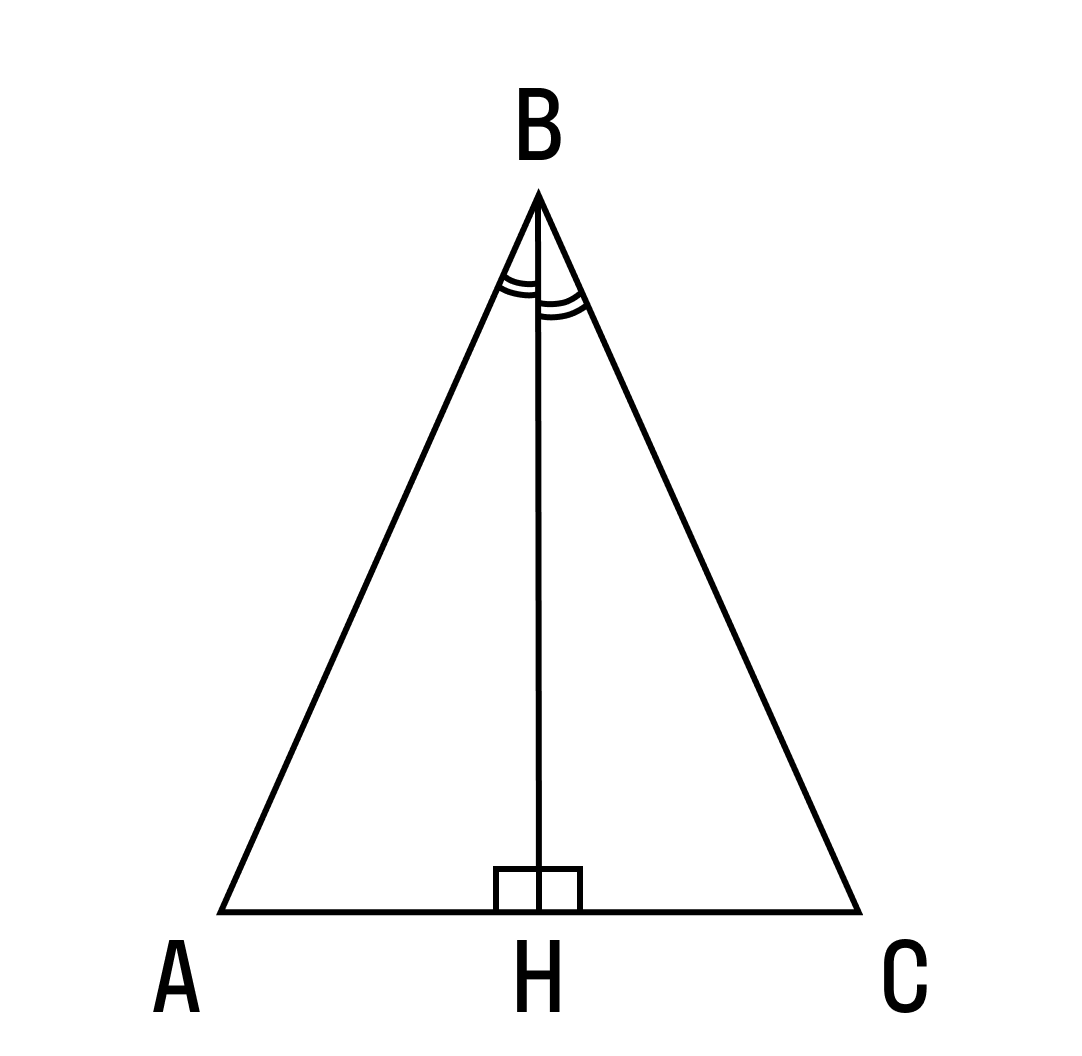
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH

Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.

А вот и доказательство:

Δ ABC
Высота BH делит Δ ABC на два прямоугольных треугольника ABH и CBH
Δ ABH = Δ CBH, поскольку гипотенузы и катет равны по теореме Пифагора
Согласно теореме 1: в треугольниках ABH и BCH ∠ BАH = ∠ BСH, поскольку углы при основании равнобедренного треугольника равны
Так как Δ ABC — равнобедренный, то его боковые стороны равны AB = BC
AH = CH, поскольку точка H делит основание Δ ABC на две равные части
Δ ABH = Δ BCH
Значит, отрезок BH одновременно биссектриса, медиана и высота равнобедренного треугольника ABC

Вуаля, сразу три теоремы доказаны.

Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).

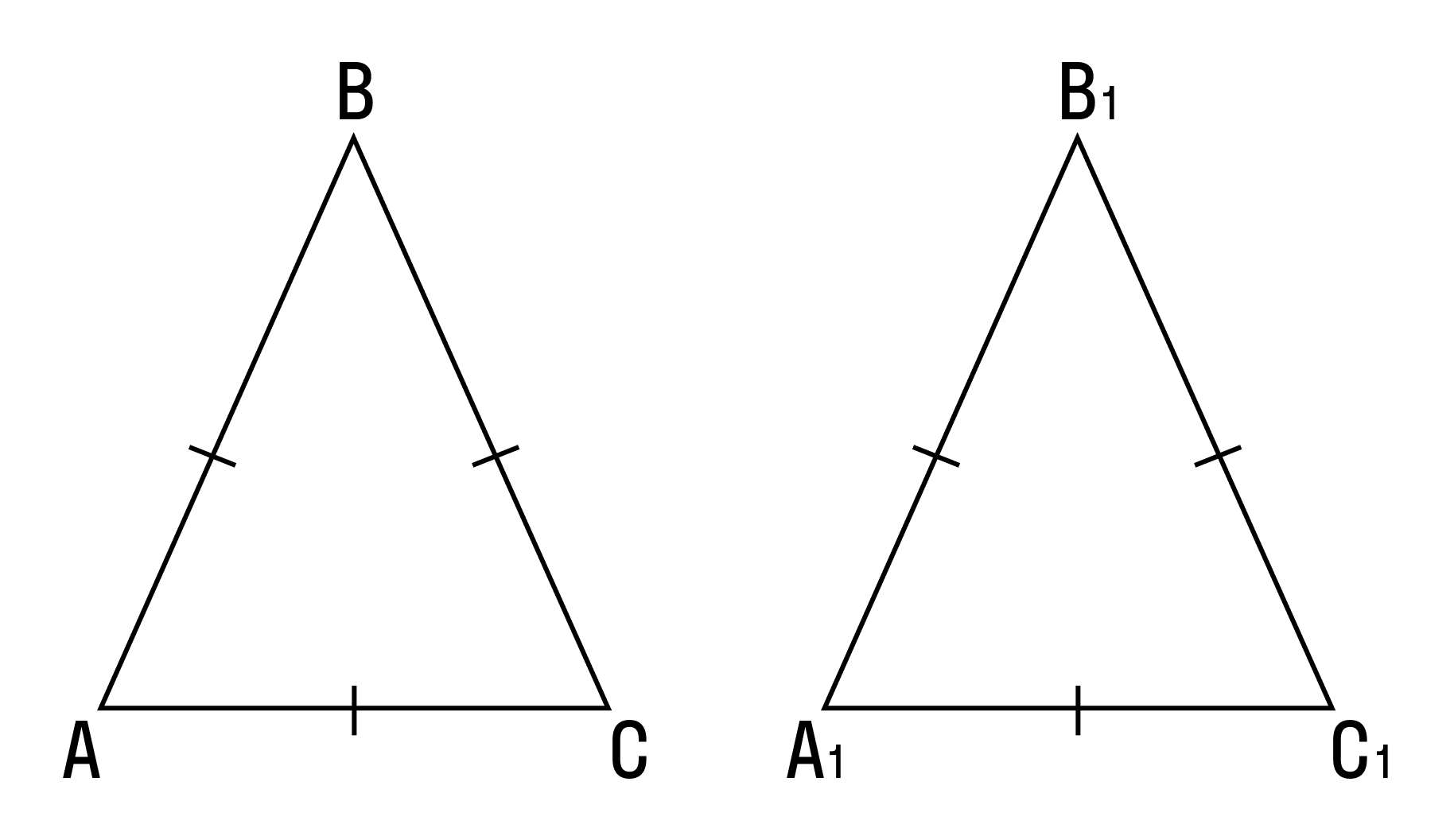
Доказательство:

Дано два Δ ABC = Δ A1B1C1.

Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.

Если все стороны совпадают — треугольники равны, а теорема доказана.

Примеры решений практических задач

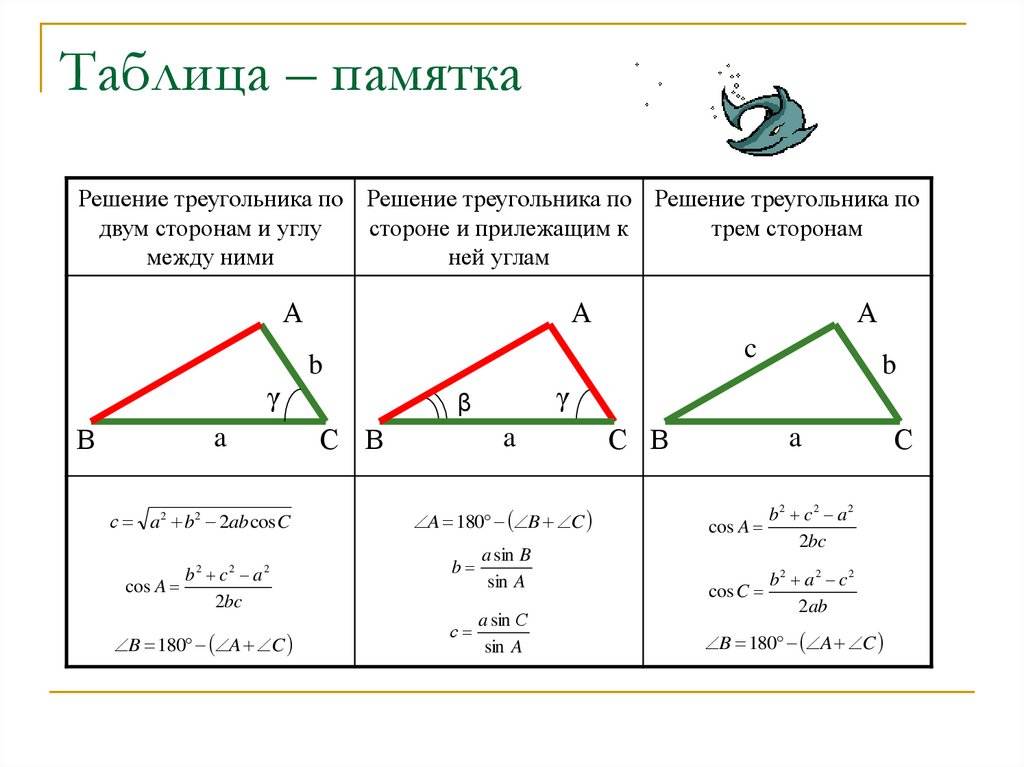
1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».

В ходе решения задачи получаем ответ: сторона c = 13,8 см; угол B = 35,2644° = 35°15’52” = 35°16′ = 0,1959π = 0,6155 rad; угол C = 84,7356° = 84°44’8” = 84°44′ = 0,4708π = 1,4789 rad; Периметр = 33,8 см; Полупериметр = 16,9 см; Площадь = 47,7984 см2; Высота h_a = 7,9664 см; Высота h_b = 11,9496 см; Высота h_c = 6,9273 см; Медиана m_a = 9,5513 см; Медиана m_b = 12,2958 см; Медиана m_c = 7,5107 см; Радиус окружности R, описанной около треугольника = 6,9291 см; Радиус окружности r, вписанной в треугольник = 2,8283 см. Таким образом, был найден угол треугольника по двум сторонам и углу.

2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».

Используя теорему косинусов, получаем угол A = 28,955° = 28°57’18” = 28°57′ = 0,1609π = 0,5054 rad; угол B = 46,5675° = 46°34’3” = 46°34′ = 0,2587π = 0,8128 rad; угол C = 104,4775° = 104°28’39” = 104°29′ = 0,5804π = 1,8235 rad; Периметр = 9 см; Полупериметр = 4,5 см; Площадь = 2,9046 см2; Высота h_a = 2,9046 см; Высота h_b = 1,9364 см; Высота h_c = 1,4523 см; Медиана m_a = 3,3912 см; Медиана m_b = 2,7839 см; Медиана m_c = 1,5811 см; Радиус окружности R, описанной около треугольника = 2,0657 см; Радиус окружности r, вписанной в треугольник = 0,6455 см.

Таким образом, были найдены все углы треугольника.

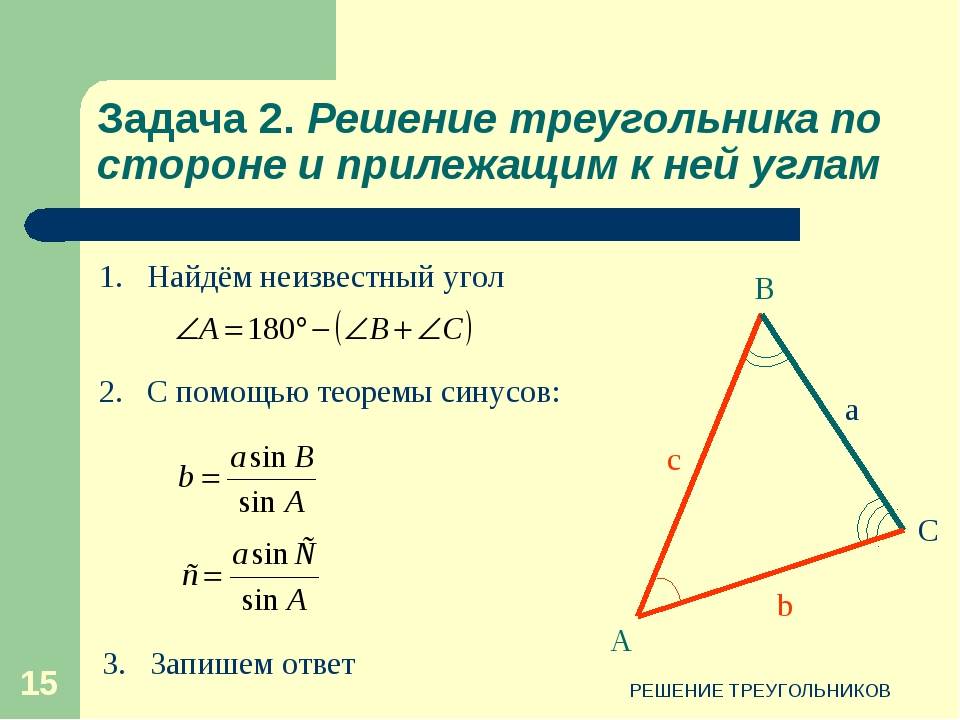
3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°. Ответ: сторона b = 2,59 см; сторона c = 3,66 см; угол A = 105° = 0,5833π = 1,8326 rad; Периметр = 11,25 см; Полупериметр = 5,625 см; Площадь = 4,5785 см2; Высота h_a = 1,8314 см; Высота h_b = 3,5355 см; Высота h_c = 2,5019 см; Медиана m_a = 1,9488 см; Медиана m_b = 4,1857 см; Медиана m_c = 3,537 см; Радиус окружности R, описанной около треугольника = 2,588 см; Радиус окружности r, вписанной в треугольник = 0,814 см.