Замеряем штангенциркулем
С помощью этого высокоточного инструмента измеряют параметры различных конструкций. Как измерить диаметр трубы штангенциркулем? Для этого нужно развести его губки, вставить в них изделие и свести так, чтобы они прижимались к поверхности. Губки при смыкании должны быть параллельны плоскости сечения трубы, иначе измерение будет неправильным. Штангенциркулем измеряют и внутренний диаметр. С его обратной стороны есть губки, которые помещаются внутрь конструкции и разводятся до примыкания к стенкам.

Смотреть галерею
Иногда требуется измерить диаметр смонтированной трубы, которая имеет слишком большие размеры. В этом случае можно измерить инструментом хорду и вычислить диаметр математическим путем. Разводим его губки на максимальное расстояние и прикладываем к трубе. Получившийся показатель – длина хорды. Для расчета понадобится также измерить высоту губок прибора. Диаметр вычисляется по формуле:
D = (2L/4H)+H.
Если губки имеют слишком большую длину, то можно подложить какую-нибудь деталь (брусок и т.д.). Тогда высота будет рассчитываться по формуле:
H = H1-H2.
Определение диаметра в бытовых условиях
До того, как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:
- рулетка или стандартная линейка;
- штангенциркуль;
- фотоаппарат – его задействуют при необходимости.
В этом случае выполняют измерение диаметра труб в такой последовательности:
- Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.
- Потом отсчитывают количество делений, соответствующих размеру диаметра.
Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров. Иногда требуется определить и площадь трубопровода, что тоже весьма просто сделать.

Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:
- Раздвигают его ножки и прикладывают к торцу изделия.
- Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.
- Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.
Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.
Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14. Не намного сложнее узнать объем трубы, выполнив простые расчеты.

Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате. Потом подставляют известные величины в формулу d=l:π, где:
d – определяемый диаметр;
l – длина измеренной окружности.
К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.
Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.

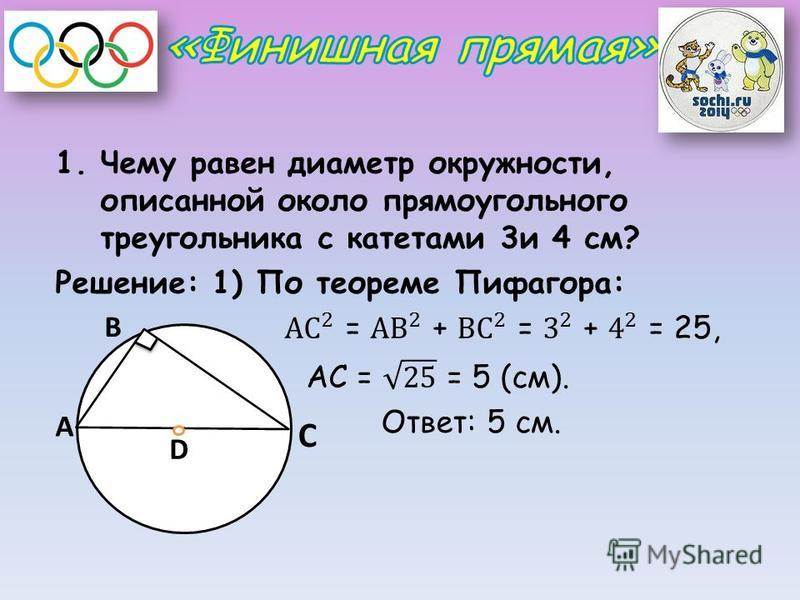
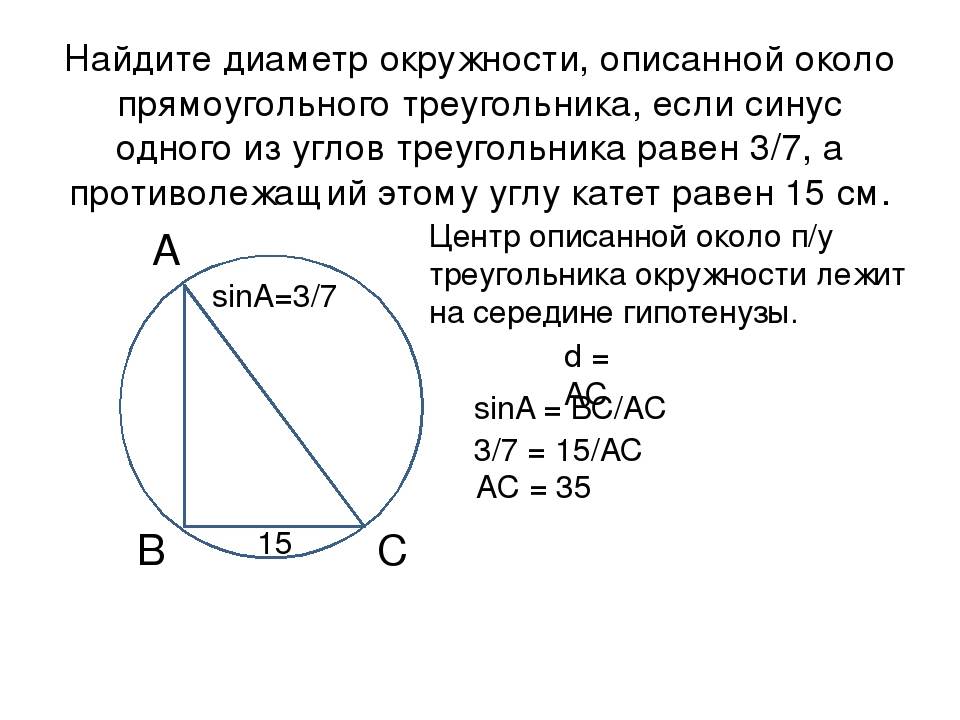
Диаметр описанной окружности
Диаметр описанной окружности также можно найти, если он описан или вписан в треугольник. Для этого сначала нужно найти радиус для вписанной окружности по формуле: R = S/p, где S обозначает площадь треугольника, а р – его полупериметр, p приравнивается к (a + b + c)/2. После того, как известен радиус, нужно воспользоваться первой формулой. Либо же сразу подставить все значения в формулу D = 2S/p.
Если вы не знаете, как найти диаметр описанной окружности, воспользуйтесь формулой, для нахождения радиуса окружности описанной около треугольника. R = (a * b * c)/4 * S, S в формуле обозначает величину площади треугольника. Потом, точно также подставьте значение радиуса в формулу D = 2R.
Внимание, только СЕГОДНЯ!
Измеряем микрометром
Высокоточные замеры (до 0,01) трубы можно сделать с помощью микрометра. Следует заметить, что им удобно измерять небольшие изделия. Инструмент представляет собой скобу, оснащенную опорной пяткой и стеблем с высокоточной резьбой (для вкручивания микровинта). На стебле можно увидеть шкалу с миллиметрами и их сотыми долями. Такое оснащение позволяет получить более точные показатели.

Смотреть галерею
Как измерить диметр трубы микрометром? Помещаем конструкцию между торцом винта и пяткой. Начинаем вращать ручку трещотки, пока она не щелкнет три раза. Сначала смотрим на нижнюю шкалу стебля, показывающую количество целых миллиметров. Проверяем наличие риски, которая находится справа. Если ее не видно, снимаем показания с барабана. Если риска есть, к получившемуся числу прибавляем 0,5 мм. Замеры по барабану определяем относительно линии на стебле между шкалами.
Об этой статье
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 139 человек(а). Количество просмотров этой статьи: 747 104.
Категории: Геометрия
English:Calculate the Circumference of a Circle
Français:calculer la circonférence d’un cercle
Italiano:Calcolare la Circonferenza di un Cerchio
Español:calcular la circunferencia
Deutsch:Einen Kreisumfang berechnen
Português:Calcular a Circunferência de um Círculo
Nederlands:De omtrek van een cirkel berekenen
中文:计算圆的周长
Bahasa Indonesia:Menghitung Keliling Lingkaran
Čeština:Jak vypočítat obvod kruhu
日本語:円の円周を計算する
ไทย:คำนวณเส้นรอบวงของวงกลม
हिन्दी:गोलाकार चीजों की परिधी ज्ञात करें
العربية:حساب محيط دائرة
Tiếng Việt:Tính Chu vi Hình tròn
한국어:원의 원주 구하는 법
Türkçe:Bir Dairenin Çevresi Nasıl Hesaplanır
فارسی:محیط یک دایره را محاسبه کنیم
Печать
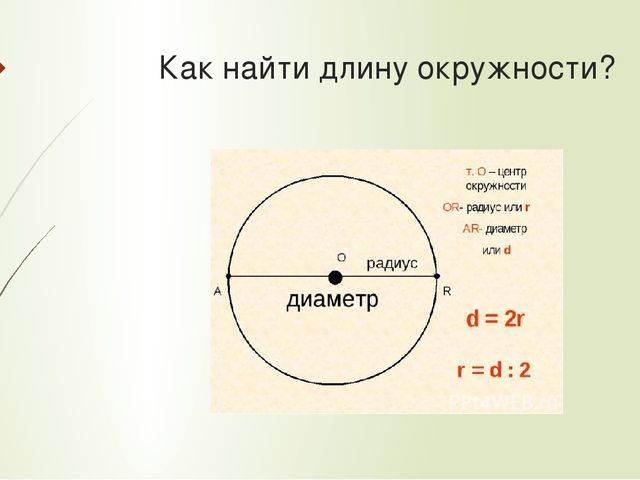
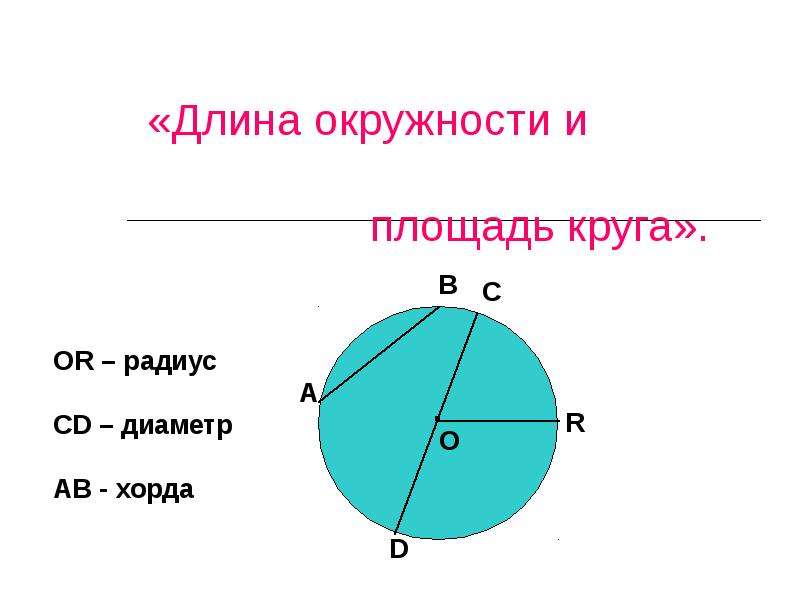
Определение длины радиуса и диаметра
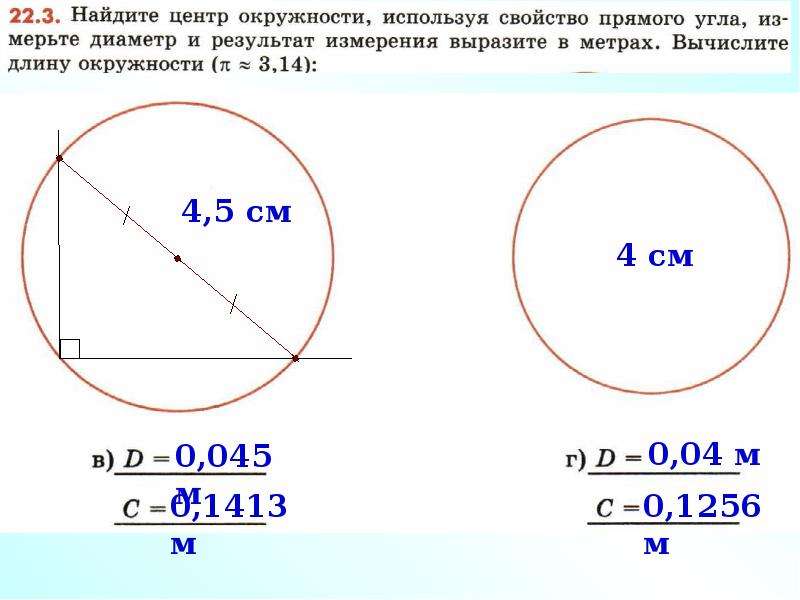
Важно! Прежде всего узнаем, как измерить диаметр. Это очень просто проводим любой радиус, продлеваем его в противоположную сторону до пересечения с дугой
Циркулем отмеряем полученное расстояние и с помощью любого метрического инструмента узнаем искомое!
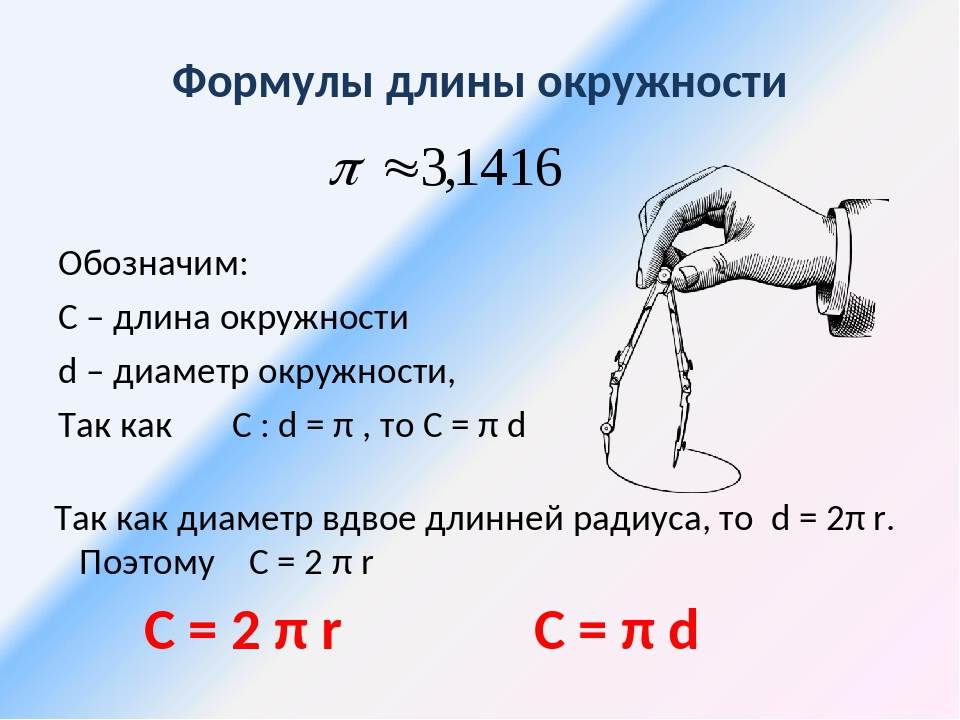
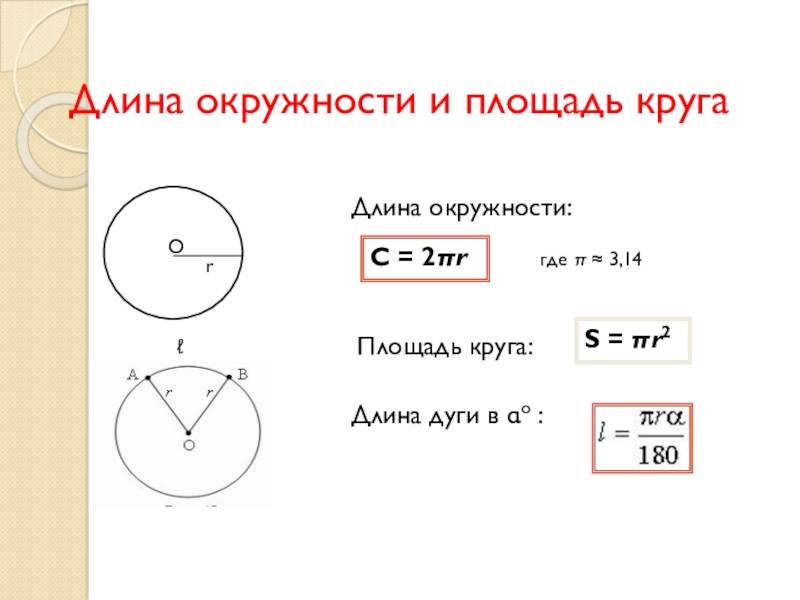
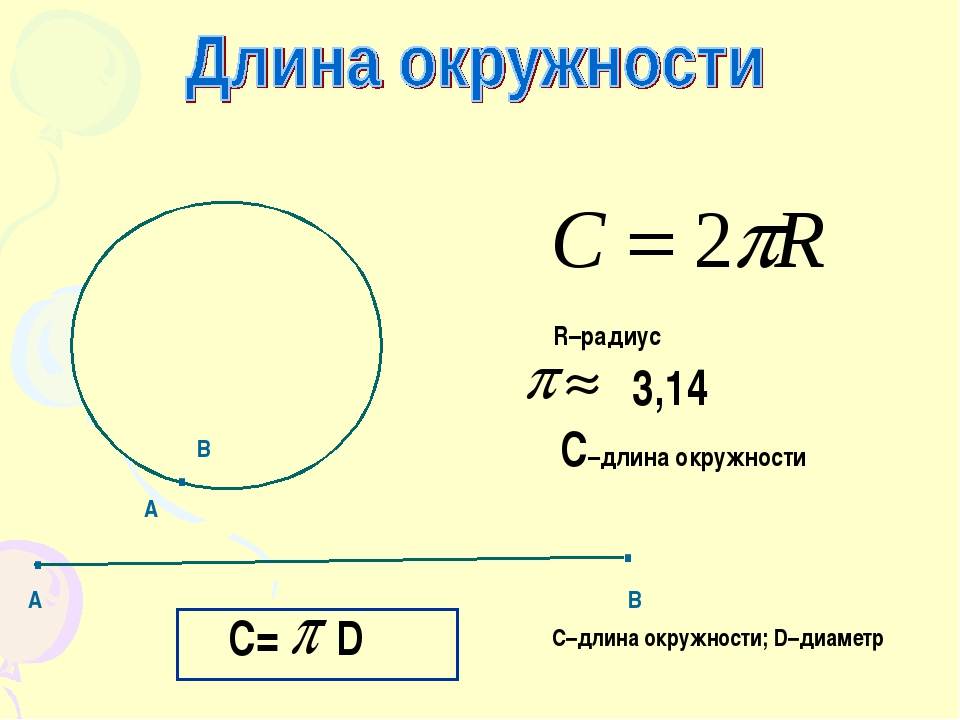
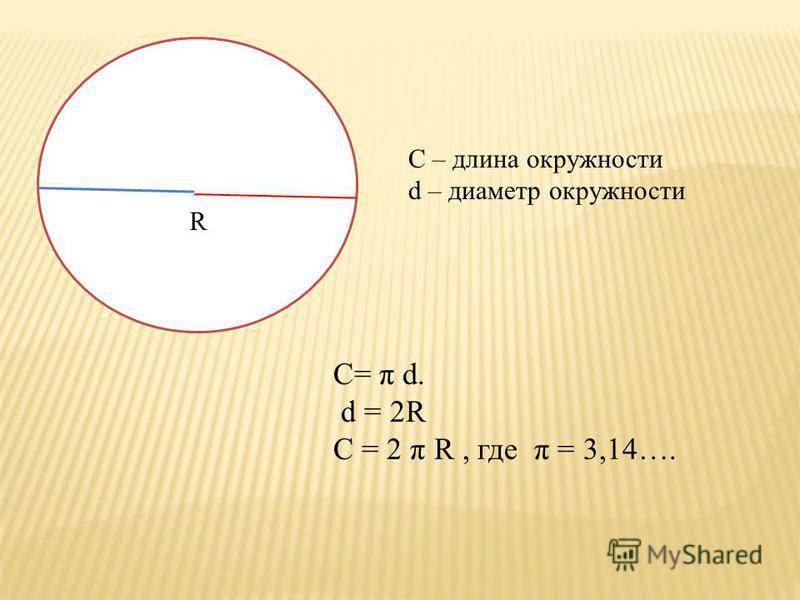
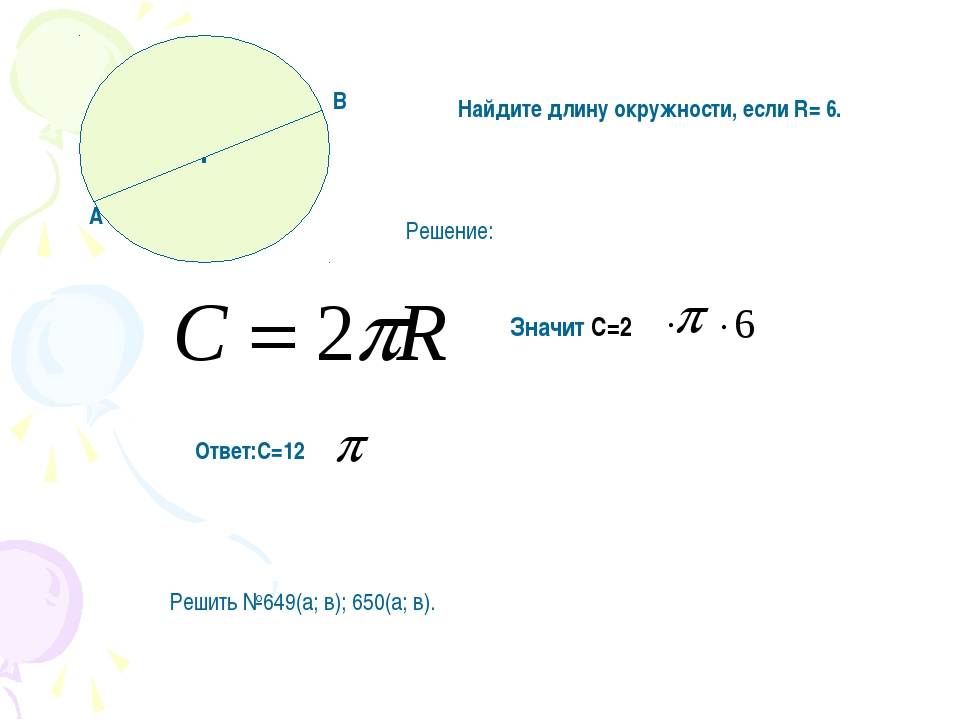
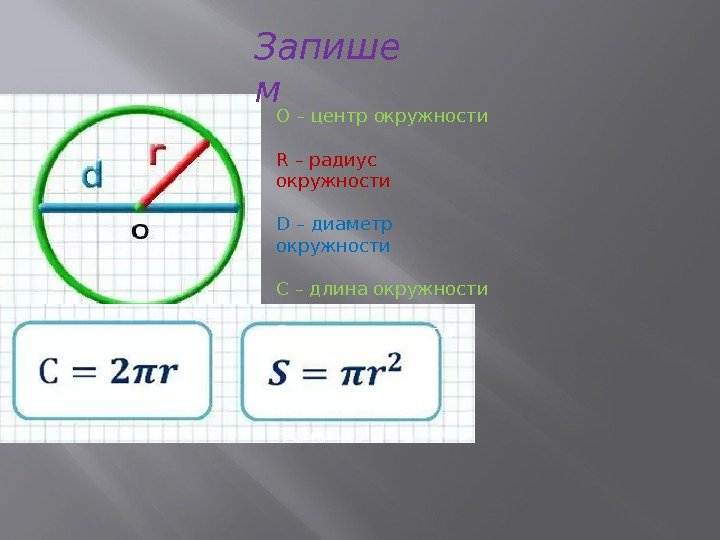
 Ответим на вопрос, как узнать диаметр окружности, зная её длину. Для этого выразим его из формулы l = П*d. Получим d = l/П.
Ответим на вопрос, как узнать диаметр окружности, зная её длину. Для этого выразим его из формулы l = П*d. Получим d = l/П.
Мы уже знаем как из длины окружности можно найти её диаметр, точно также найдём и радиус.
l = 2*П*r, отсюда r = l/2*П. Вообще, чтобы узнать радиус, его нужно выражать через диаметр и наоборот.
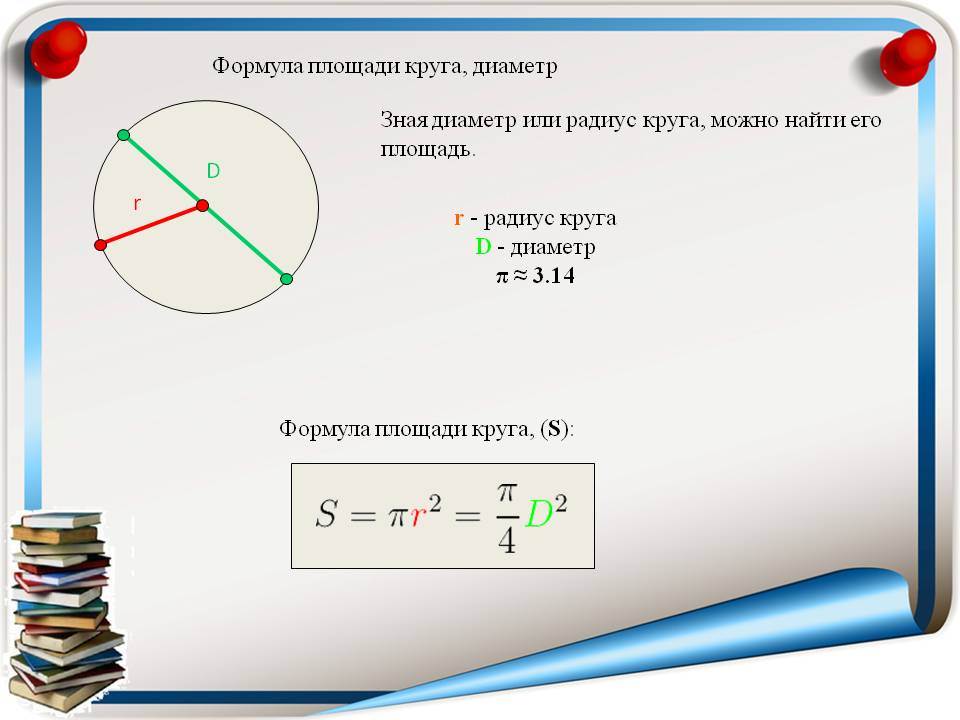
Пусть теперь требуется определить диаметр, зная площадь окружности. Используем то, что s = П*d^2/4. Выразим отсюда d. Получится d^2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие
, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
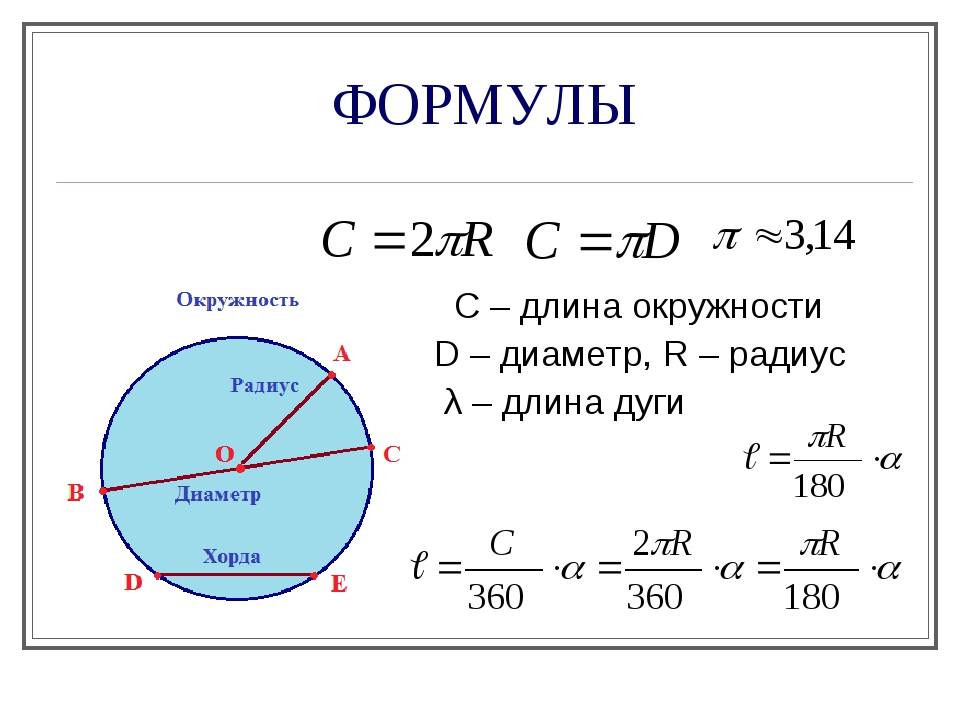
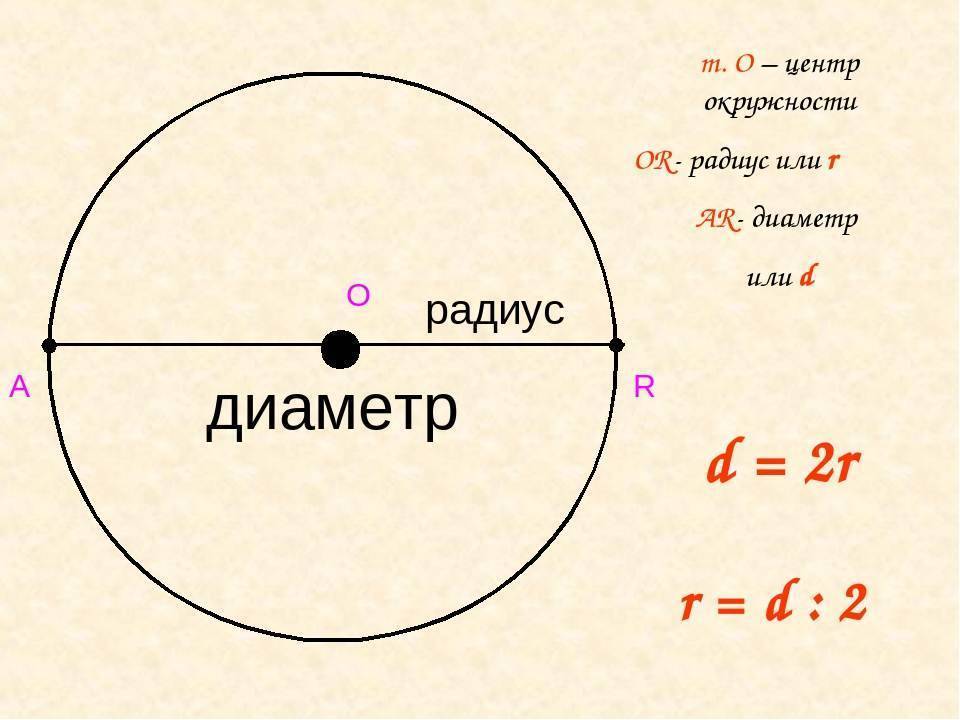
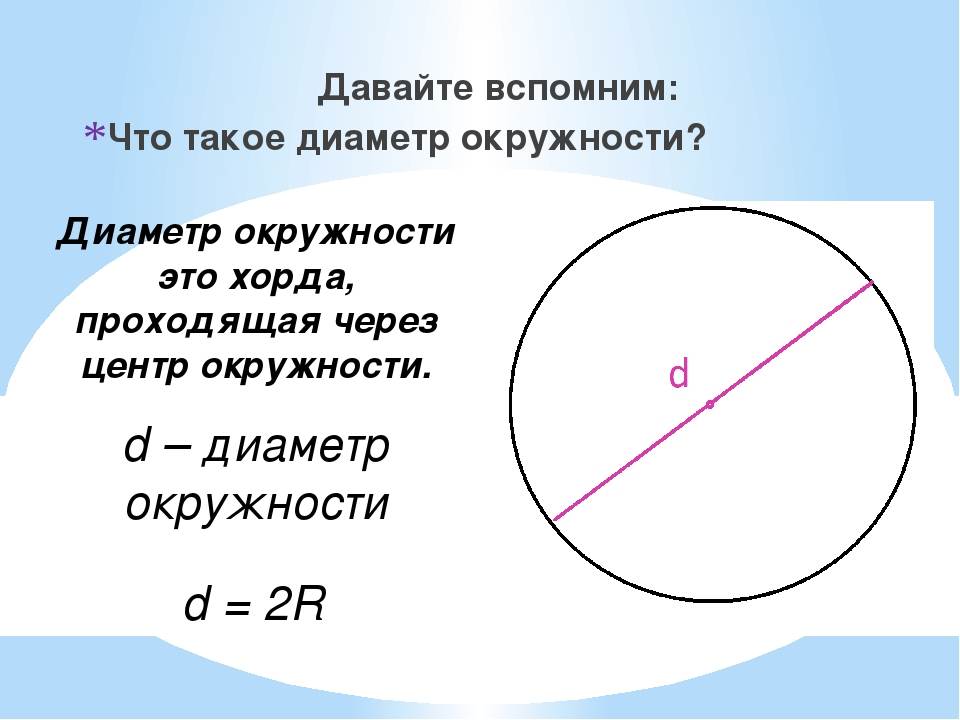
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками
, проходящее через центр фигуры.
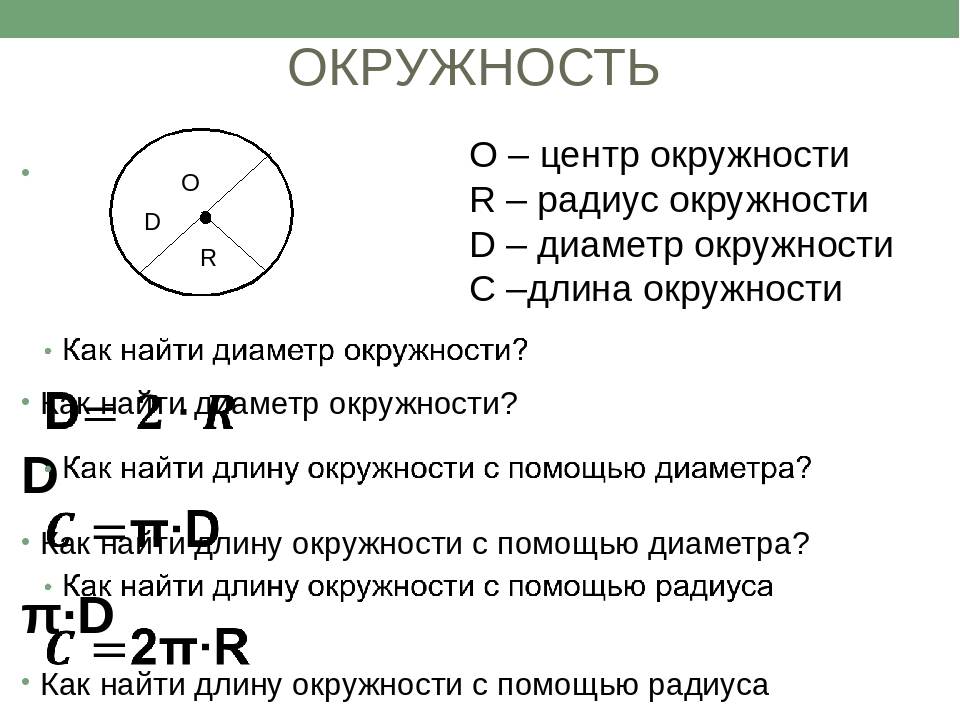
Диметр окружности
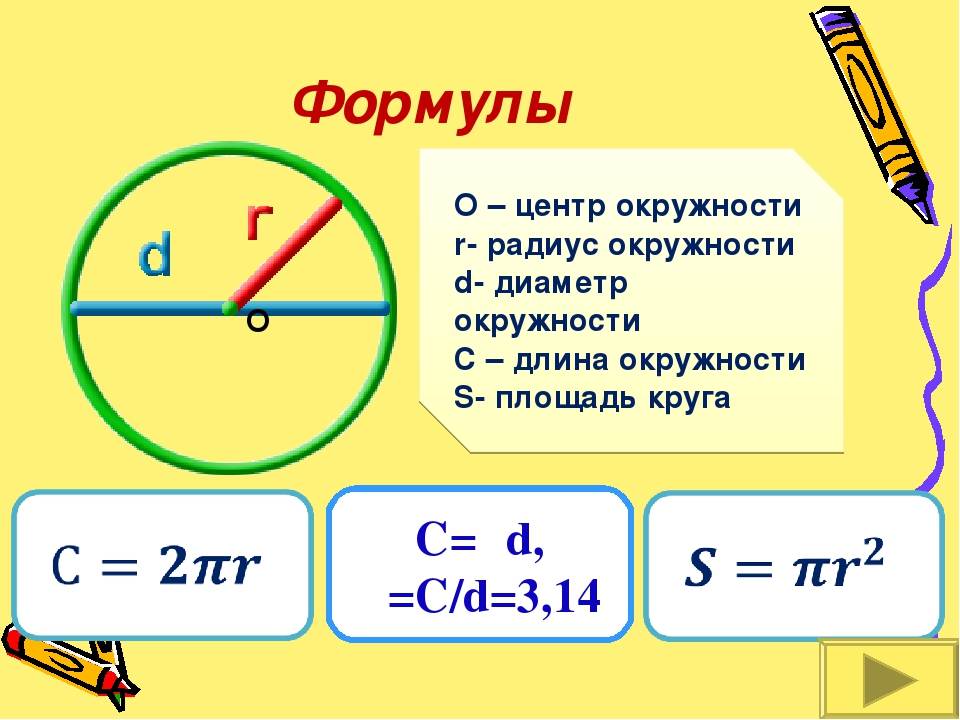
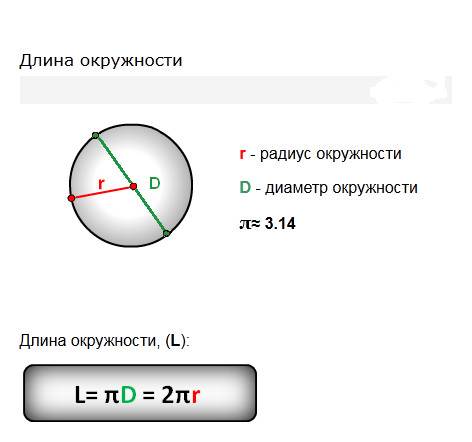
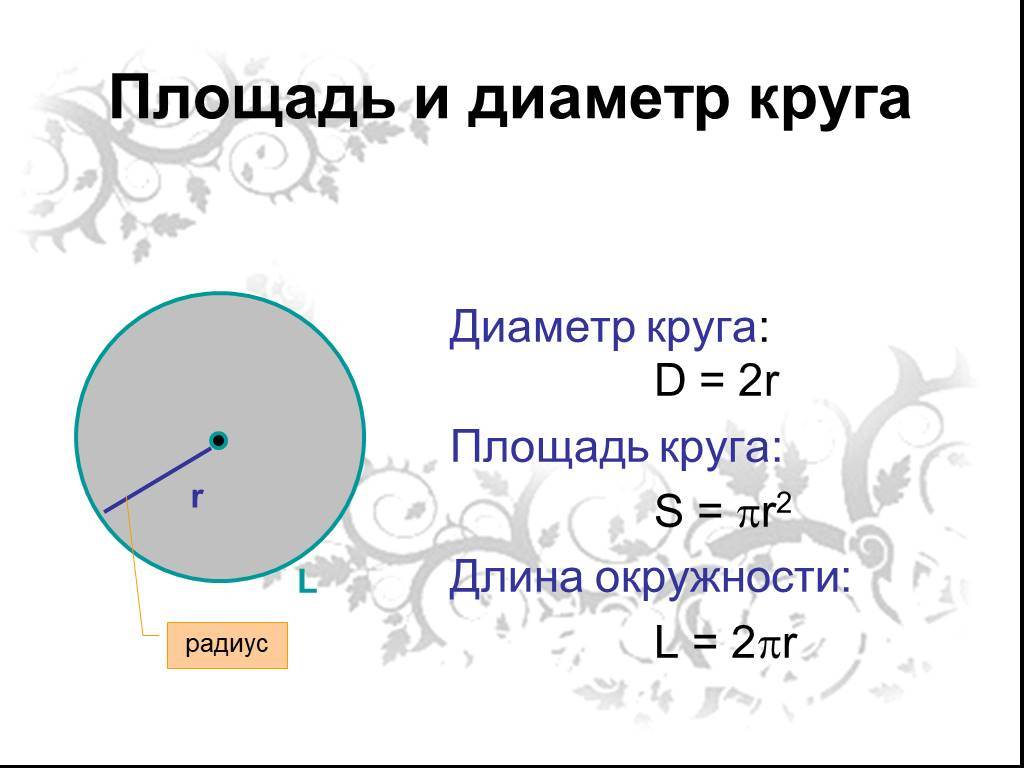
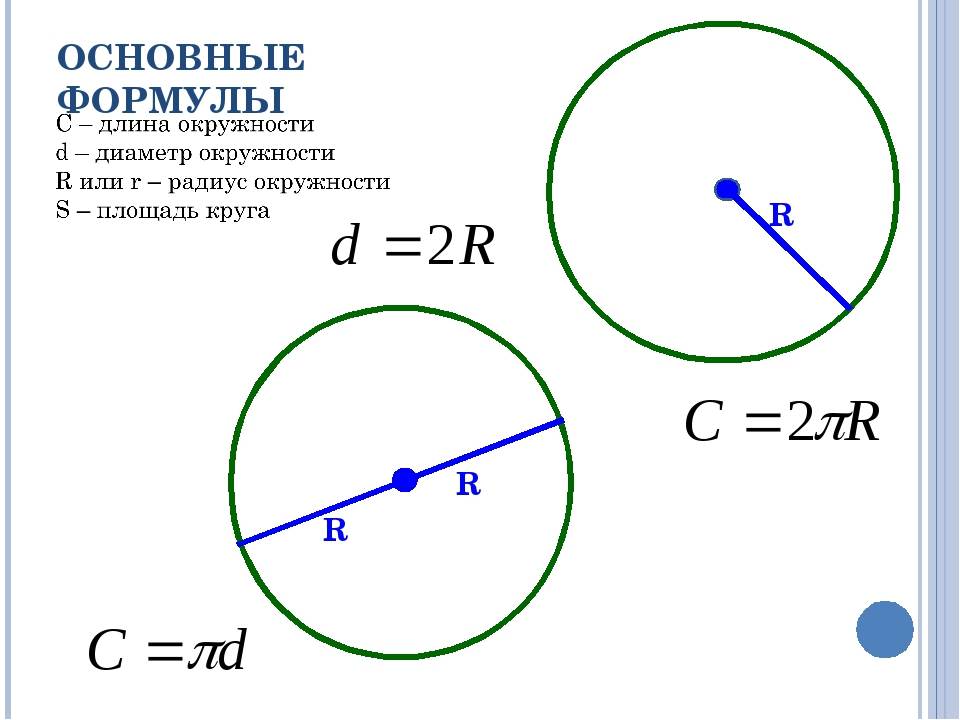
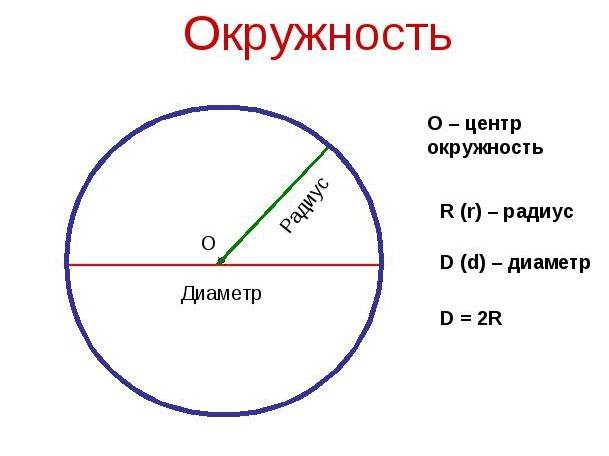
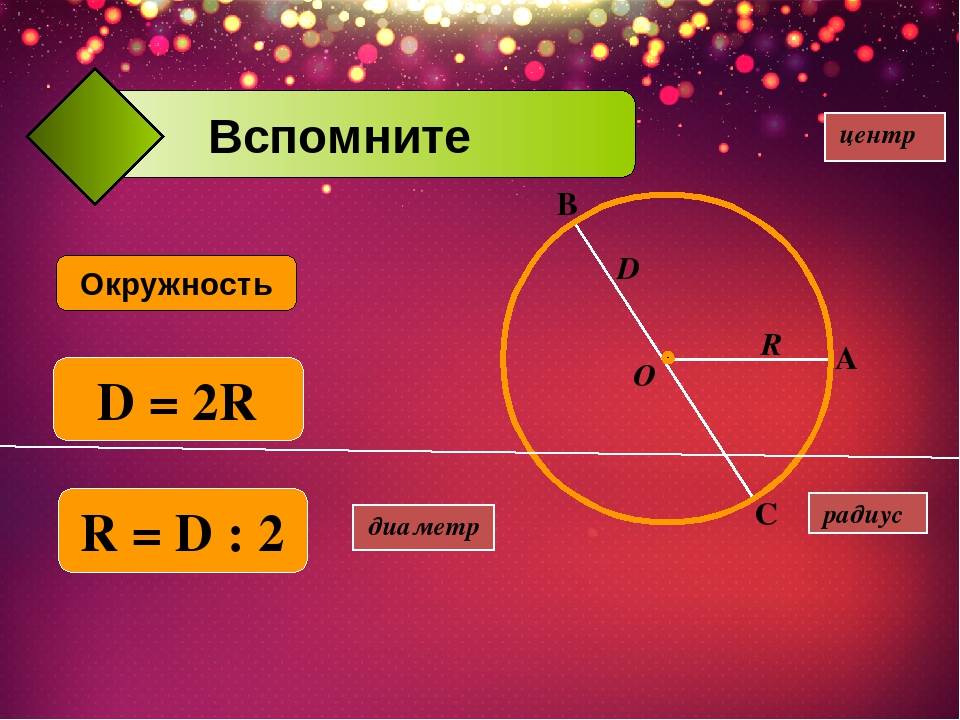
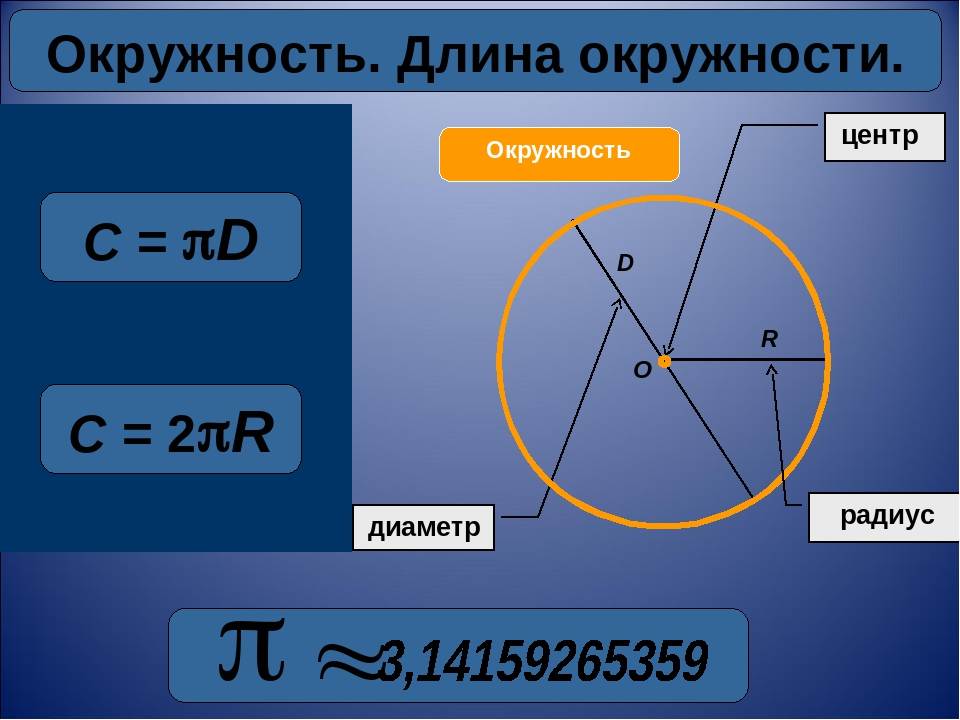
Для того, что бы знать, как найти диаметр окружности, нужно обратиться к формулам. Основных формул, по которым можно вычислить диаметр окружности две. Первая – D = 2R. Здесь диаметр равен удвоенному радиусу, где радиус – промежуток от центра до любой из точек окружности (R). Рассмотрим пример, если в задании известен радиус и он равен 10 см, то можно легко найти диаметр. Для этого значения радиуса подставим в формулу D = 2 * 10 = 20 см
Вторая формула дает возможность найти диаметр по длине окружности и выглядит она так D = L/П, где L- величина длины окружности, а П – это число Пи, которое примерно равно 3,14. Эту формулу очень удобно применять в практике. Если вам нужно знать диаметр люка, крышки на бак, какого-то котлована, стоит, лишь замерить их длину окружности и поделить ее на 3,14. Например, длина окружности равна 600 см, отсюда D = 600/3,14 = 191,08 см.
Вычисление площади круга и длины окружности, когда радиус или диаметр выражены переменными
1
Найдите радиус или диаметр окружности.
В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.
Пример: вычислите длину окружности с радиусом (х + 1).
2
Напишите формулу с данным значением.
Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.
Пример: вычислите длину окружности с радиусом (х + 1).
- Подставьте данное значение: C = 2π(х + 1)
3
Вычислите длину окружности так, как если бы переменная была представлена числом.
На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.
Пример: вычислите длину окружности с радиусом (х + 1).
- Если вы знаете значение переменной «х», подставьте его в найденное выражение, чтобы получить численный ответ.
4
Попрактикуйтесь на нескольких примерах.
Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
Найдите площадь круга с радиусом 2х. A = πr2 = π(2x)2 = π4×2 = 12,56×2
- Найдите площадь круга с диаметром (х + 2).
- A = π(d/2)2 = π((x +2)/2)2 = ((x +2)2/4)π
Совет 1: Как найти диаметр окружности, если известна длина окружности
Запишите длину окружности. диаметр которой вы намерены определить. Еще много веков назад люди брали для изготовления круглой корзины нужного размера, или диаметра, прутья в три раза более длинные.
Позже ученые доказали, что при делении длины каждой окружности на ее диаметр получается одно и то же не натуральное число. Его величина всё время уточнялась, хотя точность расчетов всегда была высока.
Например, в Древнем Египте его выражали неправильной дробью 256/8, имеющей отклонение не более одного процента.
Вспомните, что впервые математически вычислил это соотношение Архимед. Он построил правильные 96-тиугольники внутри окружности и вокруг нее.
Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419.
Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой.
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности по диаметру. Эти таблицы включают в разные справочники. Например, они есть в книге «Четырехзначные математические таблицы» В.М. Брадиса.
Совет 2: Как найти диаметр, если известна окружность
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности.
Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром.
Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Конечно, такое постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное название — это число Пи (&pi, — первая буква греческих слов «окружность » и «периметр»).
Числовое выражение этой константы определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является «иррациональным», то не имеет конечного значения — это бесконечная дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Какие бывают диаметры (+ таблица с размерами)
Важно ориентироваться не только в видах труб, но и в типах диаметра. Если взять для расчёта не те данные, из строя может выйти вся система
Чтобы не допустить распространённых ошибок, важно ознакомиться со всеми нормами и понятиями.
Крайне непрофессионально использовать исключительно теоретический диаметр трубы для проведения расчётов. Да, это удобно, быстро, но ненадёжно. Чтобы понять, как измерить диаметр, нужно определиться с тем, какой именно параметр необходимо определить. Существует несколько значений, необходимых для корректных расчётов:
- Условный проход. Это размер трубы от стенки к стенке, измеряемый в миллиметрах. При использовании дюймовой измерительной системы необходимо округление, что может негативно сказаться на точности результатов. Понятие необходимо при соединении нескольких элементов, например, трубы и фитинга.
- Толщина стенок отыгрывает далеко не последнюю роль в точности расчётов. Благодаря понятию можно легко определить прочность и надёжность системы, рассчитать максимальные нагрузки и определить пригодность трубы для той или иной сферы применения.
- Наружный диаметр – внутренний диаметр, к которому прибавлена толщина стенок.
- Номинальный диаметр – аналог условного прохода, просчитанный более точными методиками.
Измерение диаметра трубы
Важно определить, в какой единице измерения должен быть результат. Это могут быть как дюймы, так и миллиметры
Намного удобнее использование метрической системы. Подобный подход позволяет более точно определить конечные характеристики полученной системы. Несмотря на это, чаще всего используются именно дюймы. Благодаря им результат можно легко округлить, что упрощает задачу, но снижает точность показателей. Стоит отметить, что разница совершенно незначительна. Для более чёткого понимания, рекомендуется ознакомиться с размерами труб в дюймах и миллиметрах. Таблица позволит легко адаптироваться, научиться понимать незнакомые размеры. Таблица диаметров стальных труб:
| Условный диаметр | Дюймы |
| 150 | 6 |
| 200 | 8 |
| 250 | 10 |
| 300 | 12 |
| 350 | 14 |
| 400 | 16 |
| 500 | 20 |
Таблица размеров диаметров стальных труб разрабатывалась таким образом, чтобы пропускная способность увеличивалась до 50 процентов во время увеличения индекса. В целом же, 1 дюйм составляет 25,4 миллиметра. Например, 86,36 миллиметров – размер трубы в 3,4 дюйма. Диаметр трубы в 1-2 дюйма – 25,4 – 50,8 миллиметров.
Нередко можно прочесть о том, что в данной ситуации отлично подойдёт средний размер. Порой, не совсем понятно, какой размер относиться к большому, какой к маленькому. Первым делом требуется определить, какой именно диаметр указан в рекомендациях. Если речь идёт о внешних диаметрах, следует полагаться на следующие параметры:
- менее 102 – маленькие;
- 102 – 246 – средние;
- 425 и более – большие.
Внутренний диаметр зачастую не сильно отличается от внешнего, он это не означает, что его измерением можно пренебречь.
Чем толще стена – тем больше нагрузок выдержит труба. К сожалению, по-настоящему толстыми стенки бывают не часто.
Расчёт внутреннего диаметра трубы
Чтобы определить внутренние размеры, необходимо узнать внешние данные. Для этого следует взять рулетку и обвести её вокруг трубы. После полученное число следует умножить на 3,1415 (число П).
Для определения внутреннего диаметра необходимо знать толщину стенок. Данное значение необходимо умножить на 2, после чего отнять результат от внешнего диаметра.
Перед закупкой труб необходимо определить задачи, которые будет выполнять установленная система. В случае, если требуется высокая устойчивость к внутреннему давлению, лучше всего использовать бесшовный вариант. Если же нагрузки будут минимальными, выбор значительно увеличивается, шов может быть как маленьким, так и огромным. Это слабое место, которое может не выдержать серьёзного напряжения. Полагаясь на данные, полученные временем, лучше не использовать самые дешёвые варианты.
Диаметр труб также отыгрывает большую роль в дальнейшей эксплуатации. Для измерения следует воспользоваться простой формулой: длинна умноженная на число П. Если же речь о внутреннем диаметре, достаточно отнять от полученных результатов толщину стенки, умноженную на 2.
Перед приобретением трубы важно определить конкретные задачи. Если это небольшая или нерегулярная нагрузка, подойдут бюджетные варианты
В противном случае нужны исключительно бесшовные модели. Благодаря надёжной структуре такая труба не будет нуждаться в ремонте максимально длительный период.
Измерение диаметров в производственных условиях
На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю. Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Документация должна содержать определенную информацию, касающуюся труб:
- номинальные размеры;
- номер и дата ТУ;
- марка металла или вид пластика;
- номер товарной партии;
- итоги проведенных испытаний;
- хим. анализ выплавки;
- тип термической обработки;
- результаты рентгеновской дефектоскопии.

Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:
- наименование производителя;
- номер плавки;
- номер изделия и его номинальные параметры;
- дату изготовления;
- эквивалент углерода.

Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров. Для второго класса –100 миллиметров.
У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:
Δр – толщина материала рулетки;
0,2 миллиметра– припуск на прилегание инструмента к поверхности.
Допускается отклонение величины внешнего диаметра от заявленной производителем:
- для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
- для больших труб – 0,7%.
Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов.
Как вычислить диаметр: формула
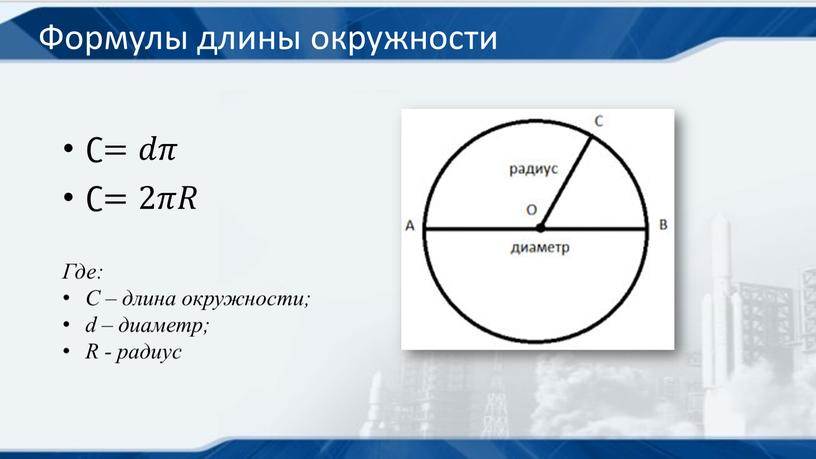
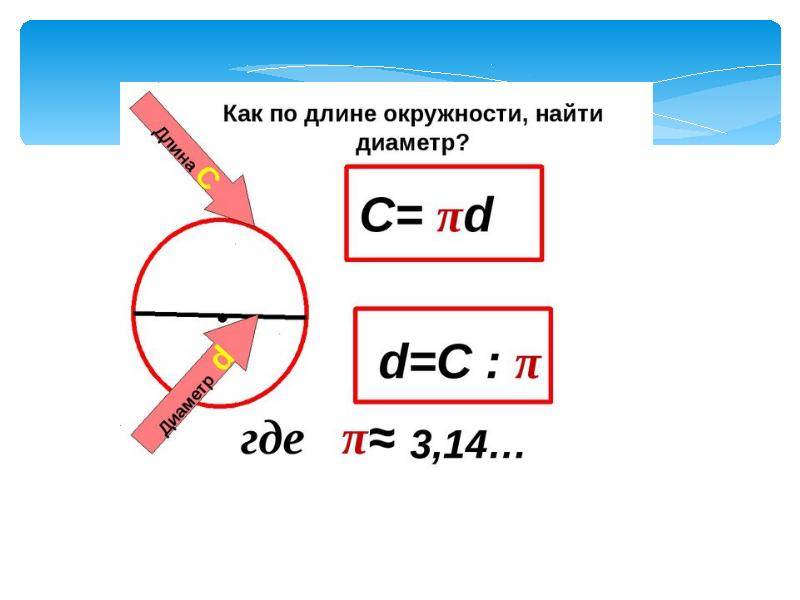
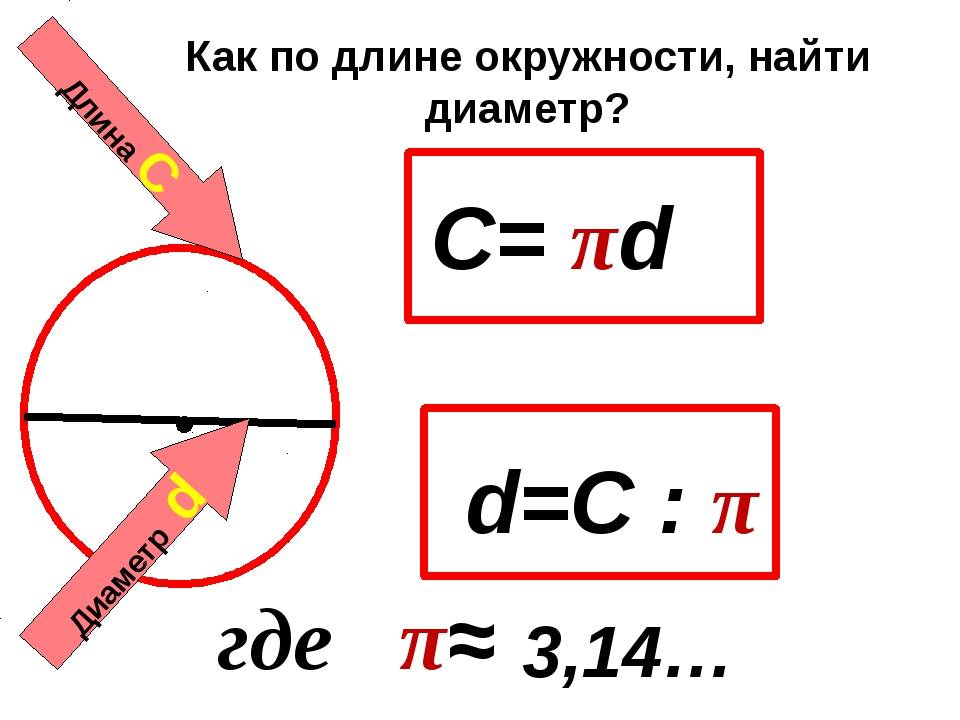
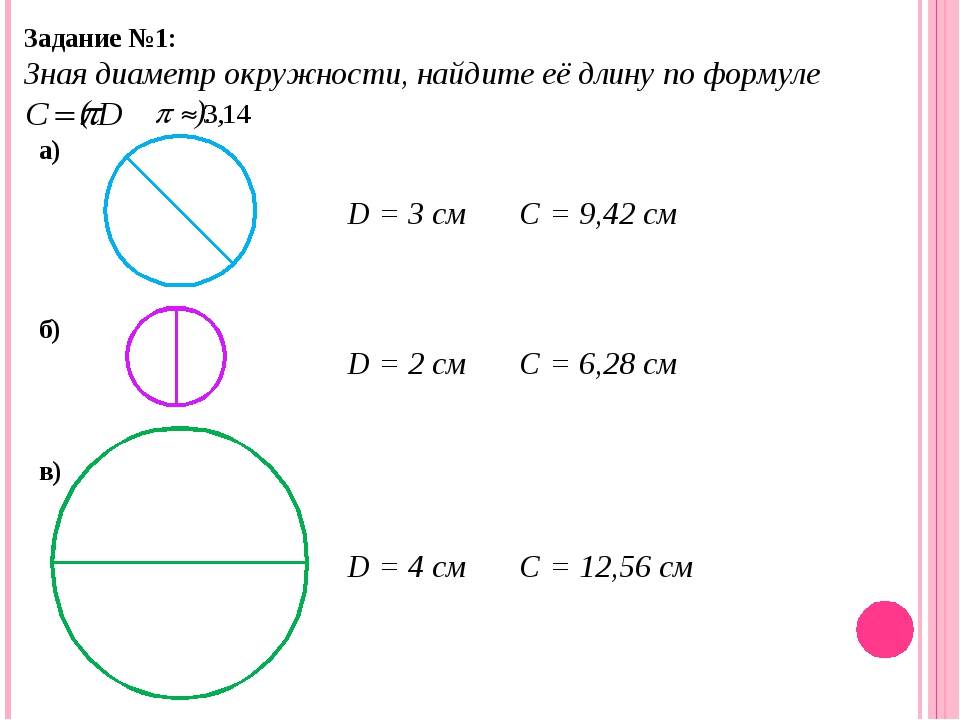
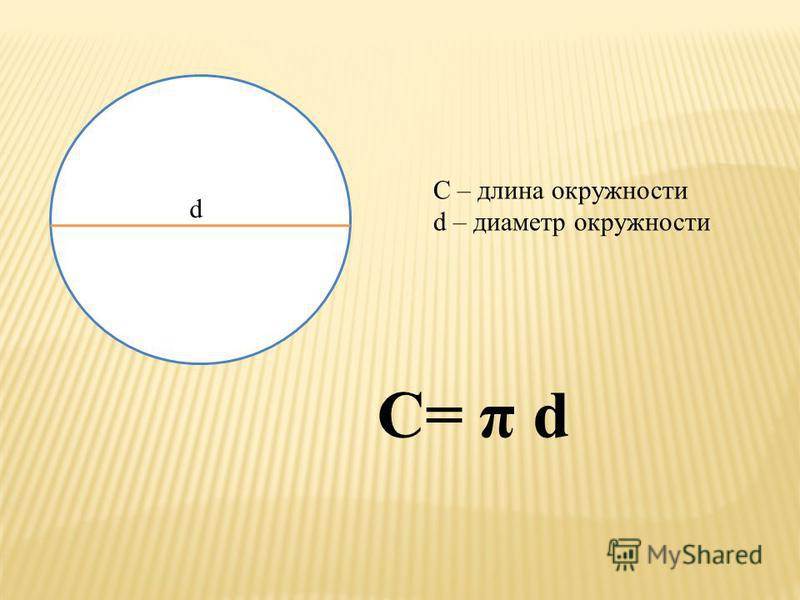
На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π. Это будет выглядеть так d = C / π.
Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас — изготовить крышку. Что будем делать в таком случае?
Нужно воспользоваться формулой. Возьмем длину очертания колодца — к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.
Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Вычисление диаметра окружности с использованием радиуса, длины окружности или площади круга
1
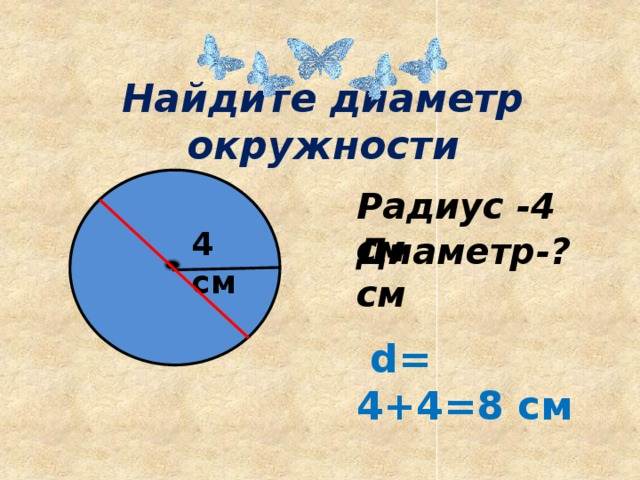
Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его.
Радиус – это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.
2
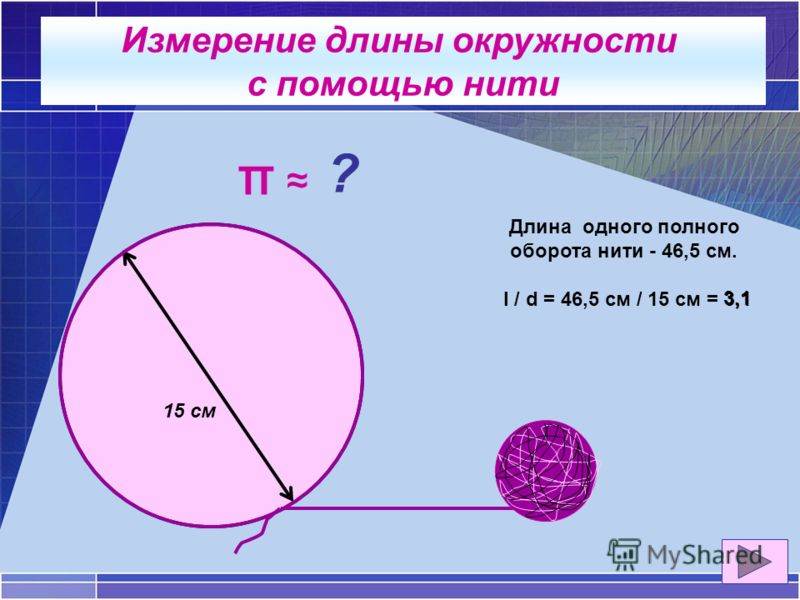
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π.
Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
3
Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра.
Данное вычисление вытекает из формулы площади круга, A = πr2, преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см2, разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.
Замеряем линейкой и рулеткой
Если на трубе видно сечение, то диаметр можно замерить обычной линейкой. Прикладываем ее к области среза так, чтобы шкала проходила ровно по центру. Берем расстояние между нужными точками (для внутреннего или наружного диаметра). Расстояние между крайними точками будет наружным диаметром. Если нужен внутренний размер, то можно узнать толщину стенок и вычесть их из получившейся цифры.

Смотреть галерею
С линейкой все ясно, а как измерить диаметр трубы рулеткой? Этот инструмент подойдет для сплошных и больших конструкций, к которым сложно подобраться. Оборачиваем изделие так, чтобы лента со шкалой плотно прилегала, и находим место ее пересечения. Получившаяся цифра – это длина окружности. Чтобы получить диаметр, разделим ее на число Пи (3,14).